题目内容
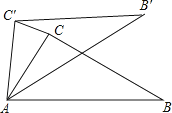
【题目】如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△BCE .
①图中哪一个点是旋转中心?
②按什么方向旋转了多少度?
③如果CF=3cm.求EF的长?
【答案】【解答】①△DCF绕点C逆时针旋转得到△BCE ,
所以旋转中心为点C;
②∵四边形ABCD为正方形,
∴CB=CD , ∠BCD=90°,
∴△DCF绕点C逆时针旋转90°得到△BCE;
③∵△DCF绕点C逆时针旋转90°得到△BCE ,
∴CE=CF , ∠ECF=90°,连接EF
∴△CEF为等腰直角三角形,
∴EF=![]() CF=
CF=![]() cm.
cm.
【解析】①②根据旋转的定义求解;③根据旋转的性质得CE=CF , ∠ECF=90°,则可判断△CEF为等腰直角三角形,然后根据等腰直角三角形的性质求解.
【考点精析】本题主要考查了旋转的性质的相关知识点,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

练习册系列答案
相关题目