题目内容
18、(1)如图所示的甲、乙两个平面图形能折什么几何体?
(2)在图丙中的适当位置添加虚线,使得它能沿虚线折叠成一个几何体.
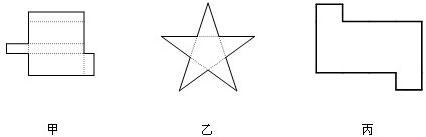
(3)若记几何体的面数为f,顶点个数为v,棱数为e,分别计算这两个几何体的f+v-e的值?
(2)在图丙中的适当位置添加虚线,使得它能沿虚线折叠成一个几何体.

(3)若记几何体的面数为f,顶点个数为v,棱数为e,分别计算这两个几何体的f+v-e的值?
分析:(1)由长方体与五棱锥的折叠及长方体与五棱锥的展开图解题.
(2)由长方体的折叠及长方体的展开图解题即可;
(3)列出几何体的面数,顶点数及棱数直接进行计算即可.
(2)由长方体的折叠及长方体的展开图解题即可;
(3)列出几何体的面数,顶点数及棱数直接进行计算即可.
解答:解:(1)图甲折叠后底面和侧面都是长方形,所以是长方体;
图乙折叠后底面是五边形,侧面是三角形,实际上是五棱锥的展开图,所以是五棱锥.
(2)所添加虚线如下所示:
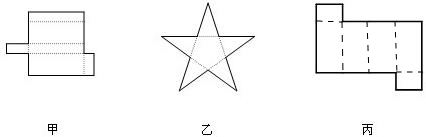
按所添虚线可以折叠成一个长方体.
(3)五棱锥的面数为6,顶点个数为6,棱数为10,f+v-e=6+6-10=2;
正方体的面数为6,顶点个数为8,棱数为12,f+v-e=6+8-12=2.
图乙折叠后底面是五边形,侧面是三角形,实际上是五棱锥的展开图,所以是五棱锥.
(2)所添加虚线如下所示:

按所添虚线可以折叠成一个长方体.
(3)五棱锥的面数为6,顶点个数为6,棱数为10,f+v-e=6+6-10=2;
正方体的面数为6,顶点个数为8,棱数为12,f+v-e=6+8-12=2.
点评:本题考查了展开图折叠成几何体的知识,有一定难度,同时考查了学生的想象和动手能力.

练习册系列答案
相关题目
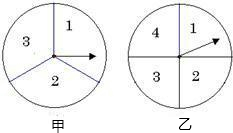 同时转动如图所示的甲,乙两个转盘,求两个转盘所转到的两个数字之和为奇数的概率(用树状图或列表法分析求解).
同时转动如图所示的甲,乙两个转盘,求两个转盘所转到的两个数字之和为奇数的概率(用树状图或列表法分析求解).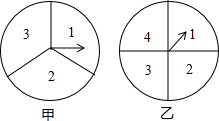 同时转动如图所示的甲、乙两个转盘,则两个转盘所转到的两个数字和为奇数的概率为( )
同时转动如图所示的甲、乙两个转盘,则两个转盘所转到的两个数字和为奇数的概率为( ) 某纸品厂要制作如图所示的甲、乙两种无盖的长方体小盒,该厂利用边角材料裁出了长方形和正方形的两种纸片,其中长方形纸片的宽与正方形纸片的边长相等,现将150张正方形纸片和300张长方形纸片用来制作这两种小盒(不计连接部分),可以做成甲、乙两种小盒各多少个?
某纸品厂要制作如图所示的甲、乙两种无盖的长方体小盒,该厂利用边角材料裁出了长方形和正方形的两种纸片,其中长方形纸片的宽与正方形纸片的边长相等,现将150张正方形纸片和300张长方形纸片用来制作这两种小盒(不计连接部分),可以做成甲、乙两种小盒各多少个?