题目内容
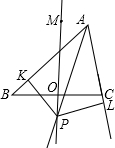 已知△ABC的角平分线AP与边BC的垂直平分线PM相交于点P,作PK⊥AB,PL⊥AC,垂足分别是K、L,
已知△ABC的角平分线AP与边BC的垂直平分线PM相交于点P,作PK⊥AB,PL⊥AC,垂足分别是K、L,
求证:BK=CL.
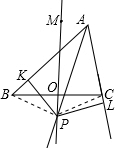 证明:连接PB,PC,
证明:连接PB,PC,∵PM垂直平分线段BC,
∴PB=PC,
∵AP平分∠BAC,PK⊥AB,PL⊥AC,
∴PK=PL,
∴△BPK≌△CPL(HL),
∴BK=CL.
分析:连接PB,PC,根据PM垂直平分线段BC可知PB=PC,已知AP平分∠BAC,PK⊥AB,PL⊥AC可知PK=PL,从而可证△BPK≌△CPL,可得BK=CL.
点评:本题考查了线段的垂直平分线性质,角平分线性质,关键是明确P点既在垂直平分线上,又在角平分线上.

练习册系列答案
相关题目
 24、已知△ABC的角平分线AP与边BC的垂直平分线PM相交于点P,作PK⊥AB,PL⊥AC,垂足分别是K、L,
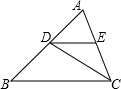
24、已知△ABC的角平分线AP与边BC的垂直平分线PM相交于点P,作PK⊥AB,PL⊥AC,垂足分别是K、L,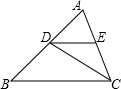 如图,已知△ABC的角平分线CD交AB于D,DE∥BC交AC于E,若DE=3,AE=4,则AC=
如图,已知△ABC的角平分线CD交AB于D,DE∥BC交AC于E,若DE=3,AE=4,则AC= 如图,已知△ABC的角平分线BD与∠ACB的外角平分线交于D点,DE∥BC交于E,交AC于F,求证:EF=BE-CF.
如图,已知△ABC的角平分线BD与∠ACB的外角平分线交于D点,DE∥BC交于E,交AC于F,求证:EF=BE-CF.