题目内容
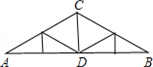
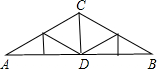如图所示，某厂车间的人字屋架为等腰三角形，跨度AB=12m，∠A=30°，则中柱CD=________m，上弦AC=________m（答案可带根号）．
分析：根据等腰三角形三线合一的性质，可求出AD的长，然后利用∠A的正切和余弦分别求出CD和AC．
解答：∵△ABC为等腰三角形，且CD为中柱，
∴CD⊥AB，BC=AC，AD=BD．
直角△ACD中，AD=AB÷2=6，∠A=30°，
∴CD=AD•tan30°=6×
=2
（m）；AC=AD÷cos30°=6÷
=4（m）．点评：本题中两个直角三角形有公共的直角边，先求出公共边是解决此类题目的基本出发点．
练习册系列答案
阅读快车系列答案
相关题目
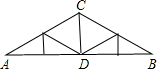如图所示，某厂车间的人字屋架为等腰三角形，跨度AB=12m，∠A=30°，则中柱CD=
