��Ŀ����
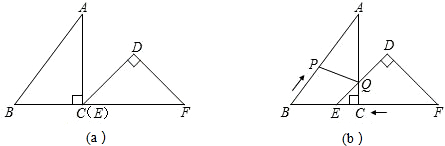
��2013•��Ϫ���ʼ죩��֪����Rt��ABC��Rt��DEF��ͼ��a���ڷţ���C���E�غϣ���B��C��E����F��ͬһ��ֱ���ϣ���ACB=��EDF=90�㣬��DEF=45�㣬AC=8���ף�BC=6���ף�EF=9���ף���ͼ��b������DEF��ͼ��a����λ�ó�������1����/����ٶ���CB���ABC�����ƶ�����Pͬʱ�ӵ�B��������2����/����ٶ���BA���A�����ƶ�������DEF�Ķ���D�ƶ���AC����ʱ�ƶ���ֹͣ����DE��AC�ཻ�ڵ�Q������PQ�����ƶ�ʱ��Ϊt���룩��0��t��4.5������
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2����tΪ��ֵʱ����APQ���ABC���ƣ�
��3����tΪ��ֵʱ����P��Q��F��ͬһֱ���ϣ�
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2����tΪ��ֵʱ����APQ���ABC���ƣ�
��3����tΪ��ֵʱ����P��Q��F��ͬһֱ���ϣ�

��������1����Ϊ��A���߶�PQ��ֱƽ�����ϣ����Եõ��߶���ȣ��ɵ�CE=CQ���ú�t��ʽ�ӱ�ʾ���������߶μ��ɵý⣻
��2����Ҫ�������ۣ���APQ�ס�ABC�͡�APQ�ס�ACB��������������������εĶ�Ӧ�߳ɱ����г���Ӧ�ı���ʽ��������߶εij��ȴ��룬����t��ֵ��
��3����P��PN��AC��N���������������Σ���PAN�ס�BAC�������������εĶ�Ӧ�߳ɱ�������
=
=
��������NQ=AQ-AN=8-t-��8-
t��=
t������QF������P��Q��F��ͬһֱ����ʱ����QCF�ס�QNP����
=
����
=
���ɴ˿������t��ֵ��
��2����Ҫ�������ۣ���APQ�ס�ABC�͡�APQ�ס�ACB��������������������εĶ�Ӧ�߳ɱ����г���Ӧ�ı���ʽ��������߶εij��ȴ��룬����t��ֵ��
��3����P��PN��AC��N���������������Σ���PAN�ס�BAC�������������εĶ�Ӧ�߳ɱ�������
| PN |
| BC |
| AP |
| AB |
| AN |
| AC |
| 8 |
| 5 |
| 3 |
| 5 |
| PN |
| FC |
| NQ |
| CQ |
6-
| ||
| 9-t |
| ||
| t |
����⣺��1�������⣬��EC=QC=t��
��BE=6-t��AQ=8-t��AB=
=10��
��BP=2t��
��AP=10-2t��
����A���߶�PQ�Ĵ�ֱƽ������ʱ��AP=AQ��
��10-2t=8-t�����t=2��
����t=2ʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2���ߡ�ACB=90�㣬
�൱��AQP=90�㼴��APQ�ס�ABCʱ��
=
����
=
�����t=0����ȥ����
����APQ=90�㼴��APQ�ס�ACBʱ��
=
����
=
�����t=3��
�൱t=3ʱ����APQ���ABC���ƣ�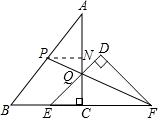
��3���������ijһʱ��t��ʹ��P��Q��F������ͬһ��ֱ���ϣ�
��P��PN��AC��N�����PAN�ס�BAC��
��
=
=
����
=
=
��
��PN=6-
t��AN=8-
t��
��NQ=AQ-AN=8-t-��8-
t��=
t��
�ߵ�P��Q��F��ͬһֱ���ϣ�
���QCF�ס�QNP��
��
=
��
��
=
��
���t=1
�൱t=1ʱ��P��Q��F������ͬһֱ���ϣ�
��BE=6-t��AQ=8-t��AB=
| BC2+AC2 |
��BP=2t��
��AP=10-2t��
����A���߶�PQ�Ĵ�ֱƽ������ʱ��AP=AQ��
��10-2t=8-t�����t=2��
����t=2ʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2���ߡ�ACB=90�㣬
�൱��AQP=90�㼴��APQ�ס�ABCʱ��
| AQ |
| AP |
| AC |
| AB |
| 8-t |
| 10-2t |
| 4 |
| 5 |
����APQ=90�㼴��APQ�ס�ACBʱ��
| AP |
| AQ |
| AC |
| AB |
| 10-2t |
| 8-t |
| 4 |
| 5 |
�൱t=3ʱ����APQ���ABC���ƣ�

��3���������ijһʱ��t��ʹ��P��Q��F������ͬһ��ֱ���ϣ�
��P��PN��AC��N�����PAN�ס�BAC��
��
| PN |
| BC |
| AP |
| AB |
| AN |
| AC |
| PN |
| 6 |
| 10-2t |
| 10 |
| AN |
| 8 |
��PN=6-
| 6 |
| 5 |
| 8 |
| 5 |
��NQ=AQ-AN=8-t-��8-
| 8 |
| 5 |
| 3 |
| 5 |
�ߵ�P��Q��F��ͬһֱ���ϣ�
���QCF�ס�QNP��
��
| PN |
| FC |
| NQ |
| CQ |
��
6-
| ||
| 9-t |
| ||
| t |
���t=1
�൱t=1ʱ��P��Q��F������ͬһֱ���ϣ�
���������⿼�������������ε��ж������ʡ����κ�������ֵ������ͼ�ε��������֪ʶ��ͼ�νϸ��ӣ�����ѧ�����ν�ϵ��������ۺ���ǿ���ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
 ��2013•��Ϫ���ʼ죩��ͼ��������ABCD�ı߳�Ϊ2��E��CD���е㣬�ڶԽ���AC����һ��P����PD+PE����Сֵ��
��2013•��Ϫ���ʼ죩��ͼ��������ABCD�ı߳�Ϊ2��E��CD���е㣬�ڶԽ���AC����һ��P����PD+PE����Сֵ��