题目内容
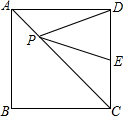（2013•安溪县质检）如图，正方形ABCD的边长为2，E是CD的中点，在对角线AC上有一点P，则PD+PE的最小值是| 5 |
| 5 |
分析：连接BE，甴正方形的性质可知点B、D关于直线AC对称，故BE即是PD+PE的最小值，根据勾股定理即可得出BE的长．
解答：
解：连接BE，
∵四边形ABCD是正方形，E是CD的中点，
∴点B、D关于直线AC对称，CE=
CD=1，
∴BE即是PD+PE的最小值，
∴BE=
=
=
．
故答案为：
．
解：连接BE，∵四边形ABCD是正方形，E是CD的中点，
∴点B、D关于直线AC对称，CE=
| 1 |
| 2 |
∴BE即是PD+PE的最小值，
∴BE=
| BC2+CE2 |
| 22+12 |
| 5 |
故答案为：
| 5 |
点评：本题考查的是轴对称-最短路线问题，熟知“两点之间，线段最短”是解答此题的关键．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目