题目内容
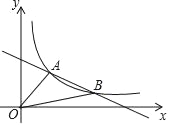
【题目】如图,一次函数y1=﹣![]() x+4的图象与反比例函数y2=
x+4的图象与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点
的图象交于A(2,3),B(6,n)两点
(1)观察图象当y1>y2时,x的取值范围是 ;
(2)求反比例函数的解析式及B点坐标;
(3)求△OAB的面积.
【答案】(1)x<0或2<x<6;(2)y2=![]() ,(6,1);(3)8.
,(6,1);(3)8.
【解析】
(1)观察函数图象得到当x<0或2<x<6时,一次函数图象在反比例函数图象的上方;
(2)把A(2,3)代入y2=![]() ,利用待定系数法求反比例函数的解析式;将B(6,n)代入y1=﹣
,利用待定系数法求反比例函数的解析式;将B(6,n)代入y1=﹣![]() x+4可求出n的值,即可求出B点坐标;
x+4可求出n的值,即可求出B点坐标;
(3)求得直线与x轴的交点坐标,根据三角形面积公式即可求得.
解:(1)根据图象可知,当y1>y2时,x的取值范围是x<0或2<x<6.
故答案为x<0或2<x<6;

(2)把A(2,3)代入y2=![]() ,得m=2×3=6,
,得m=2×3=6,
∴反比例函数的解析式为y2=![]() ;
;
将B(6,n)代入y1=﹣![]() x+4,
x+4,
得n=﹣![]() ×6+4=1,
×6+4=1,
∴B点坐标为(6,1);
(3)由直线y1=﹣![]() x+4可知与x轴的交点为(8, 0),
x+4可知与x轴的交点为(8, 0),
又∵A(2,3),B(6,1),
∴S△AOB=![]() ×8×3﹣
×8×3﹣![]() ×8×1=8.
×8×1=8.

【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?