题目内容
如图，在平面直角坐标系中有一矩形ABCD，其中A（0，0），B （8，0），D （0，4），若将△ABC沿AC所在直线翻折，点B落在点E处．则E点的坐标是 ▲ ．
（
,
）
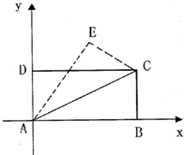
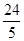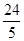,）连接BE，与AC交于G，作EF⊥AB，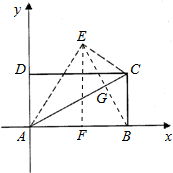
∵AB=AE，∠BAC=∠EAC，
∴△AEB是等腰三角形，AG是BE边上的高，∴EG=GB，EB=2EG，
BG=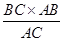
=
，
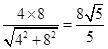设E（x，y），则有：AE2-AF2=BE2-BF2即：82-x2=（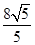
）2-（8-x）2，
解得：x=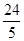，y=EF=，∴E点的坐标为：（,）．
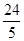∵AB=AE，∠BAC=∠EAC，
∴△AEB是等腰三角形，AG是BE边上的高，∴EG=GB，EB=2EG，
BG=
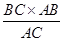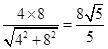=，设E（x，y），则有：AE2-AF2=BE2-BF2即：82-x2=（
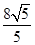）2-（8-x）2，解得：x=
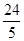，y=EF=，∴E点的坐标为：（,）．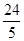
练习册系列答案
相关题目
在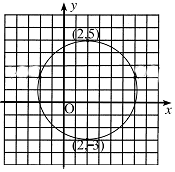
）
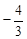