Question

一节数学课后，老师布置了一道课后练习题：

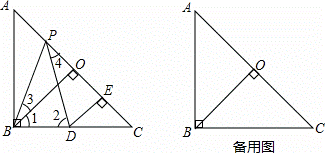
如图，已知在Rt△ABC中，AB=BC，∠ABC=90°，BO⊥AC，于点O，点PD分别在AO和BC上，PB=PD，DE⊥AC于点E，求证：△BPO≌△PDE．

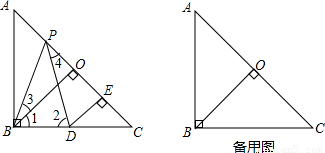
（1）理清思路，完成解答（2）本题证明的思路可用下列框图表示：

根据上述思路，请你完整地书写本题的证明过程．

（2）特殊位置，证明结论

若PB平分∠ABO，其余条件不变．求证：AP=CD．

（3）知识迁移，探索新知

若点P是一个动点，点P运动到OC的中点P′时，满足题中条件的点D也随之在直线BC上运动到点D′，请直接写出CD′与AP′的数量关系．（不必写解答过程）

 

Answer 1

【答案】

（1）求出∠3=∠4，∠BOP=∠PED=90°，根据AAS证△BPO≌△PDE即可；

（2）求出∠ABP=∠4，求出△ABP≌△CPD，即可得出答案；

（3）设OP=CP=x，求出AP=3x，CD=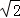x，即可得出答案．

【解析】（1）证明：∵PB=PD，

∴∠2=∠PBD，

∵AB=BC，∠ABC=90°，

∴∠C=45°，

∵BO⊥AC，

∴∠1=45°，

∴∠1=∠C=45°，

∵∠3=∠PBO﹣∠1，∠4=∠2﹣∠C，

∴∠3=∠4，

∵BO⊥AC，DE⊥AC，

∴∠BOP=∠PED=90°，

在△BPO和△PDE中

∴△BPO≌△PDE（AAS）；

（2）证明：由（1）可得：∠3=∠4，

∵BP平分∠ABO，

∴∠ABP=∠3，

∴∠ABP=∠4，

在△ABP和△CPD中

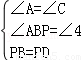
∴△ABP≌△CPD（AAS），

∴AP=CD．

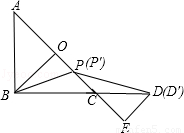
（3）解：CD′与AP′的数量关系是CD′=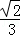AP′．

理由是：设OP=PC=x，则AO=OC=2x=BO，

则AP=2x+x=3x，

由（2）知BO=PE，

PE=2x，CE=2x﹣x=x，

∵∠E=90°，∠ECD=∠ACB=45°，

∴DE=x，由勾股定理得：CD=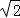x，

即AP=3x，CD=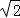x，

∴CD′与AP′的数量关系是CD′=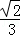AP′