题目内容
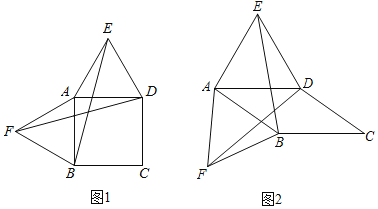
【题目】如图,以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接BE、DF.
(1)当四边形ABCD为正方形时(如图1),则线段BE与DF的数量关系是 .
(2)当四边形ABCD为平行四边形时(如图2),问(1)中的结论是否还成立?若成立,请证明;若不成立,请说明理由.
【答案】(1)BE=DF(或相等);(2)成立.证明见解析.
【解析】
(1)根据正方形的性质和等边三角形性质得:AB=AD,∠BAD=90°,AF=AB,AE=AD,∠BAF=∠DAE=60°,再根据全等三角形判定和性质即可.
(2)先利用平行四边形性质和等边三角形性质,再运用全等三角形判定和性质即可.
解:(1)BE=DF(或相等)如图1,

∵四边形ABCD为正方形
∴AB=AD,∠BAD=90°
∵△ABF、△ADE都是等边三角形
∴AF=AB,AE=AD,∠BAF=∠DAE=60°
∴∠BAE=∠BAD+∠DAE=150°,∠DAF=∠BAD+∠BAF=150°
∴∠BAE=∠DAF
∵AB=AF=AE=AD
∴△ABE≌△AFD(SAS)
∴BE=DF
故答案为:BE=DF或相等;
(2)成立.
证明:如图2,

∵△AFB为等边三角形
∴AF=AB,∠FAB=60°
∵△ADE为等边三角形,
∴AD=AE,∠EAD=60°
∴∠FAB+∠BAD=∠EAD+∠BAD,
即∠FAD=∠BAE.
在△AFD和△ABE中,
 ,
,
∴△AFD≌△ABE(SAS),
∴BE=DF.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了从甲、乙两名同学中选拔一人参加射击比赛,在同等的条件下,教练给甲、乙两名同学安排了一次射击测验,每人打10发子弹.下表是甲、乙两人各自的射击情况记录(其中乙的记录表上射中9,10环的子弹数被墨水污染看不清楚,但是教练记得乙射中9,10环的子弹数均不为0发).
甲
中靶环数(环) | 5 | 6 | 8 | 9 | 10 |
射中此环的子弹数(发) | 4 | 1 | 3 | 1 | 1 |
乙
中靶环数(环) | 5 | 6 | 7 | 9 | 10 |
射中此环的子弹数(发) | 2 | 3 | 2 |
(1)求甲同学在这次测验中平均每次射中的环数;
(2)从这次测验的平均成绩的角度考虑,如果你是教练,你认为选谁参加比赛比较合适?并说明理由.