Question

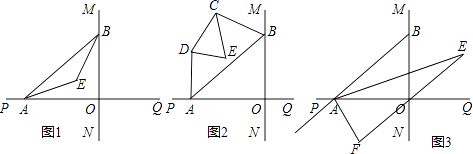
【题目】（10分）已知△ABC和△ADE是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE中点，连结DF、CF.

（1）如图1， 当点D在AB上，点E在AC上，请直接写出此时线段DF、CF的数量关系和位置关系（不用证明）；

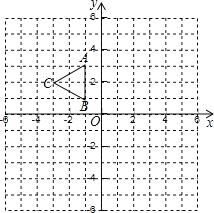
（2）如图2，在（1）的条件下将△ADE绕点A顺时针旋转45°时，请你判断此时（1）中的结论是否仍然成立，并证明你的判断；

（3）如图3，在（1）的条件下将△ADE绕点A顺时针旋转90°时，若AD=1，AC=，求此时线段CF的长（直接写出结果）.

Answer 1

【答案】（1）相等和垂直；（2）成立，理由见试题解析；（3）．

【解析】

试题分析：（1）根据“直角三角形斜边上的中线等于斜边的一半”可知DF=BF，根据∠DFE=2∠DCF，∠BFE=2∠BCF，得到∠EFD+∠EFB=2∠DCB=90°，DF⊥BF．

（2）延长DF交BC于点G，先证明△DEF≌△GCF，得到DE=CG，DF=FG，根据AD=DE，AB=BC，得到BD=BG又因为∠ABC=90°，所以DF=CF且DF⊥BF．

（3）延长DF交BA于点H，先证明△DEF≌△HBF，得到DE=BH，DF=FH，根据旋转条件可以△ADH为直角三角形，由△ABC和△ADE是等腰直角三角形，AC=，可以求出AB的值，进而可以根据勾股定理可以求出DH，再求出DF，由DF=BF，求出得CF的值．

试题解析：（1）∵∠ACB=∠ADE=90°，点F为BE中点，∴DF=BE，CF=BE，∴DF=CF．

∵△ABC和△ADE是等腰直角三角形，∴∠ABC=45°，

∵BF=DF，∴∠DBF=∠BDF，

∵∠DFE=∠ABE+∠BDF，∴∠DFE=2∠DBF，

同理得：∠CFE=2∠CBF，

∴∠EFD+∠EFC=2∠DBF+2∠CBF=2∠ABC=90°，∴DF=CF，且DF⊥CF．

（2）（1）中的结论仍然成立．

证明：如图，此时点D落在AC上，延长DF交BC于点G．

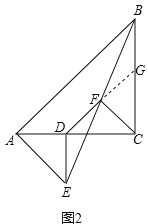
∵∠ADE=∠ACB=90°，∴DE∥BC．∴∠DEF=∠GBF，∠EDF=∠BGF．

∵F为BE中点，∴EF=BF．∴△DEF≌△GBF．∴DE=GB，DF=GF．

∵AD=DE，∴AD=GB，

∵AC=BC，∴AC﹣AD=BC﹣GB，∴DC=GC．

∵∠ACB=90°，∴△DCG是等腰直角三角形，

∵DF=GF，∴DF=CF，DF⊥CF．

（3）延长DF交BA于点H，

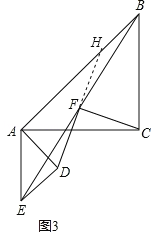
∵△ABC和△ADE是等腰直角三角形，∴AC=BC，AD=DE．∴∠AED=∠ABC=45°，

∵由旋转可以得出，∠CAE=∠BAD=90°，

∵AE∥BC，∴∠AEB=∠CBE，∴∠DEF=∠HBF．

∵F是BE的中点，∴EF=BF，∴△DEF≌△HBF，∴ED=HB，

∵AC=，在Rt△ABC中，由勾股定理，得：AB=4，

∵AD=1，∴ED=BH=1，∴AH=3，在Rt△HAD中由勾股定理，得：DH=，

∴DF=，∴CF=，∴线段CF的长为．