Question

【题目】分别以□ABCD（∠CDA≠90°）的三边AB，CD，DA为斜边作等腰直角三角形，△ABE，△CDG，△ADF．
（1）如图1，当三个等腰直角三角形都在该平行四边形外部时，连接GF，EF．请判断GF与EF的关系（只写结论，不需证明）；
（2）如图2，当三个等腰直角三角形都在该平行四边形内部时，连接GF，EF，（1）中结论还成立吗？若成立，给出证明；若不成立，说明理由．

Answer 1

【答案】解：（1）GF⊥EF，GF=EF。

（2）GF⊥EF，GF=EF成立。理由如下：

∵四边形ABCD是平行四边形，∴AB=CD，∠DAB+∠ADC=180°。

∵△ABE，△CDG，△ADF都是等腰直角三角形，

∴DG=CG=AE=BE，DF=AF，∠CDG=∠ADF=∠BAE=45°

∴∠BAE+∠FDA+∠EAF+∠ADF+∠FDC=180°。∴∠EAF+∠CDF=45°。

∵∠CDF+∠GDF=45°，∴∠FDG=∠EAF。

∵在△EAF和△GDF中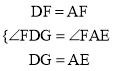， ，∴△EAF≌△GDF（SAS）。

∴EF=FG，∠EFA=∠DFG，即∠GFD+∠GFA=∠EFA+∠GFA。

∴∠GFE=90°。∴GF⊥EF。

【解析】试题分析：根据等腰直角三角形的性质和平行四边形的性质来证明△FDG和△FAE全等，从而得到FG=EF，∠DFG=∠AFE，根据∠DFA=90°得出∠GFE=90°，即EF⊥FG.

试题解析：（1）答：在图1中，GF=EF且GE⊥EF

(2)、∵四边形ABCD是平行四边形

∴AB=DC，且AB∥DC． 又∵△ABE、△CDG是等腰三角形

∴AE=BE=DG=CG，∠CDG=∠BAE=45°

又∵△AFD是等腰三角形，

∴AF=DF，∠FDA=∠DAF=45°，∠AFD=90°

又∵AB∥DC ∴∠CDA+∠DAB=180°

又∵∠CDA=90°-∠FDG；∠DAB=90°+∠FAE

∴90°-∠FDG+90°+∠FAE=180°

∴∠FDG=∠FAE

∴△FDG≌△FAE（SAS）．

∴FG=FE，∠DFG=∠AFE

又∵∠DFG+∠GFA=90°，

∴∠AFE+∠GFA=90°．

∴EE⊥GF