题目内容
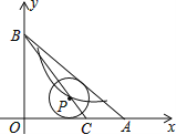
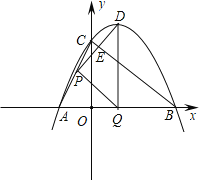
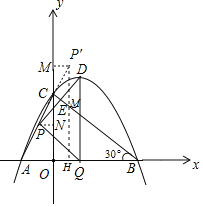
【题目】如图,抛物线y=ax2+bx+3![]() 与x轴交于A(﹣3,0),B(9,0)两点,与y轴交于点C,连接AC,BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ,过点Q作QD⊥x轴,与抛物线交于点D,连接PD与BC交于点E.设点P的运动时间为t秒(t>0)
与x轴交于A(﹣3,0),B(9,0)两点,与y轴交于点C,连接AC,BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ,过点Q作QD⊥x轴,与抛物线交于点D,连接PD与BC交于点E.设点P的运动时间为t秒(t>0)
(1)求抛物线的表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简).
②在点P,Q运动的过程中,当PQ=PD时,求t的值;
(3)点M为线段BC上一点,在点P,Q运动的过程中,当点E为PD中点时,是否存在点M使得PM+![]() BM的值最小?若存在,请求出PM+
BM的值最小?若存在,请求出PM+![]() BM的最小值;若不存在,请说明理由.
BM的最小值;若不存在,请说明理由.
![]()
【答案】(1)![]() ;(2)P
;(2)P  ,D
,D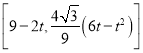 ;
;
![]() ;(3)存在,故PM+
;(3)存在,故PM+![]() BM的最小值为
BM的最小值为![]() .
.
【解析】
(1)把A(﹣3,0),B(9,0)两点,代入解析式即可
(2)先求出BC的解析式①把P,Q代入解析式即可解答
②当PQ=PD时,则DQ中点的纵坐标=点P的纵坐标,在代入解析式即可
(3)根据点E是PQ的中点,求出点E的坐标,将其代入解析式②即可求出P,作点P关于直线BC的对称点P′,过点P′作P′H⊥x轴、BC于点H、M,过点P作PN⊥y轴于点N,再证明△P′MC≌△PNC(AAS),即可解答
解:(1)将A(﹣3,0),B(9,0)代入y=ax2+bx+3![]() ,得:
,得:
![]() ,解得:
,解得: ,
,
∴抛物线的表达式为y=﹣![]() x2+
x2+![]() x+3
x+3![]() ①;
①;
(2)由题意得:∠ACO=∠OBC=30°,∠ACB=90°,
将点B、C(0,3![]() )的坐标代入一次函数表达式并解得:
)的坐标代入一次函数表达式并解得:
直线BC的表达式为:y=﹣![]() x+3
x+3![]() ②;
②;
①点P的坐标为(﹣3+![]() t,
t,![]() t),
t),
点Q(9﹣2t,0),将点Q的坐标代入①式并整理得:点D[9﹣2t,![]() (6t﹣t2)];
(6t﹣t2)];
②当PQ=PD时,则DQ中点的纵坐标=点P的纵坐标,
即:![]() [
[![]() (6t﹣t2)]=
(6t﹣t2)]=![]() t,
t,
解得:t=![]() ;
;
(3)点P的坐标为(﹣3+![]() t,
t,![]() t)、点D[9﹣2t,
t)、点D[9﹣2t,![]() (6t﹣t2)],
(6t﹣t2)],
点E是PQ的中点,则点E[3﹣![]() t,
t,![]() t+
t+![]() (6t﹣t2)],
(6t﹣t2)],
将点E的坐标代入②式并整理得:t2﹣6t+9=0,解得:t=3,
即点P(﹣![]() ,
,![]() )即点P是AC的中点,
)即点P是AC的中点,
作点P关于直线BC的对称点P′,过点P′作P′H⊥x轴、BC于点H、M,过点P作PN⊥y轴于点N,
则MH=![]() MB,
MB,
则此时,PM+![]() BM=PM+MH=P′H为最小值,
BM=PM+MH=P′H为最小值,
∵∠ACB=90°,PC=P′C,∠P′CM=∠NCP,∠P′MC=∠PNC=90°,
∴△P′MC≌△PNC(AAS),∴MC=NC=![]() OC,
OC,
OM=![]() OC=
OC=![]() =P′H,
=P′H,
故PM+![]() BM的最小值为
BM的最小值为![]() .
.

 阅读快车系列答案
阅读快车系列答案