题目内容
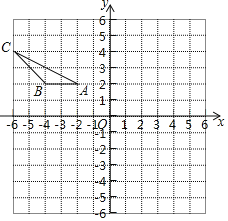
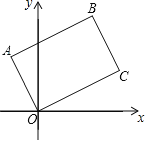
【题目】将矩形OABC如图放置，O为原点，若点A的坐标是（﹣1，2），点B的坐标是（2，
），则点C的坐标是（ ）
A. （4，2）B. （2，4）C. （
，3）D. （3，）
【答案】D
【解析】
首先构造直角三角形，利用相似三角形的判定与性质以及结合全等三角形的判定与性质得出CM＝
，MO＝3，进而得出答案．
解：如图：过点A作AE⊥x轴于点E，过点B作BF⊥⊥x轴于点F，过点A作AN⊥BF于点N，
过点C作CM⊥x轴于点M，
∵∠EAO+∠AOE＝90°，∠AOE+∠MOC＝90°，
∴∠EAO＝∠COM，
又∵∠AEO＝∠CMO，
∴∠AEO∽△COM，
∴
，
∵∠BAN+∠OAN＝90°，∠EAO+∠OAN＝90°，
∴∠BAN＝∠EAO＝∠COM，
在△ABN和△OCM中
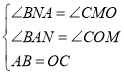
∴△ABN≌△OCM（AAS），
∴BN＝CM，
∵点A（﹣1，2），点B的纵坐标是
，
∴BN＝，
∴CM＝，
∴MO＝3，
∴点C的坐标是：（3，）．
故选：D．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
