题目内容
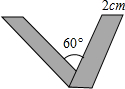
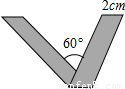
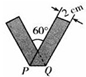同学们在拍照留念的时候最喜欢做一个“V”字型的动作．我们将宽为| 1 | 2 |
分析：首先过点O作OD⊥CQ于D，由折叠的性质，可求得OD的值，然后利用三角函数的性质，求得O的长，同理可得OP的长，即可证得△OPQ是等边三角形，则问题得证．
解答：解：过点O作OD⊥CQ于D，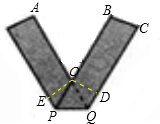
∴OD=BC=2cm，∠DOP=∠ODQ=90°，
∵∠POQ=∠AOB=60°，
∴∠QOD=∠DOP-∠POQ=30°，
∴cos∠DOQ=cos30°=
=
=
，
∴OQ=
cm，
同理：OP=
cm，
∴OQ=OP，
∴△OPQ是等边三角形，
∴PQ=
cm．
故答案为：
．
∴OD=BC=2cm，∠DOP=∠ODQ=90°，
∵∠POQ=∠AOB=60°，
∴∠QOD=∠DOP-∠POQ=30°，
∴cos∠DOQ=cos30°=
| OD |
| OQ |
| 2 |
| OQ |
| ||
| 2 |
∴OQ=
4
| ||
| 3 |
同理：OP=
4
| ||
| 3 |
∴OQ=OP，
∴△OPQ是等边三角形，
∴PQ=
4
| ||
| 3 |
故答案为：
4
| ||
| 3 |
点评：此题考查了翻折变换的性质．注意折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等，解题的关键是注意辅助线的作法，注意数形结合思想的应用．
练习册系列答案
相关题目
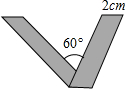同学们在拍照留念的时候最喜欢做一个“V”字型的动作．我们将宽为2cm的长方形如图进行翻折，便可得到一个漂亮的“V”．如果“V”所成的锐角为60°，那么折痕AQ长是
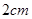的长方形如图进行翻折，便可得到一个漂亮的“V”。如果“V”所成的锐角为600，那么折痕
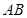的长是 。
