题目内容
已知等腰梯形的周长为64，腰长为8，对角线长为28，则连接两腰中点与一底中点的线段组成的三角形的周长为 ．
【答案】分析：根据已知条件画出图形，利用等腰梯形的性质及三角形中位线的性质求解即可．
解答：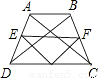
解：∵等腰梯形的周长为64，腰长为8，
∴AB+CD=64-8-8=48，
∵点E，F，G分别是AD，BC，DC的中点，AC=BD=28，
∴EG=FG=
AC=14，EF=
（AB+CD）=24，
∴△EFG的周长=14+14+24=52．
点评：此题主要考查学生对等腰梯形的性质及三角形中位线的理解及运用．
解答：
解：∵等腰梯形的周长为64，腰长为8，∴AB+CD=64-8-8=48，
∵点E，F，G分别是AD，BC，DC的中点，AC=BD=28，
∴EG=FG=
AC=14，EF=（AB+CD）=24，∴△EFG的周长=14+14+24=52．
点评：此题主要考查学生对等腰梯形的性质及三角形中位线的理解及运用．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目