��Ŀ����
����Ŀ����1�����֣���ͼ1����AΪ�߶�BC��һ���㣬��BC=a��AB=b��
����գ�����Aλ���� ��ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪ�� �����ú�a��b��ʽ�ӱ�ʾ��
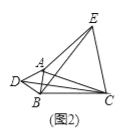
��2��Ӧ�ã���AΪ�߶�BC��һ���㣬��BC=3��AB=1����ͼ2��ʾ���ֱ���AB��ACΪ�ߣ����ȱ�������ABD�͵ȱ�������ACE������CD��BE��
�����ҳ�ͼ����BE��ȵ��߶Σ���˵�����ɣ�
��ֱ��д���߶�BE�������ֵ��

���𰸡���1��CB���ӳ����ϣ�a+b����2����CD=BE�����ɼ����������߶�BE�������ֵΪ4�����ɼ�����.
�������������������1�����ݵ�AΪ�߶�BC��һ���㣬��BC=a��AB=b���ɵõ���Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪBC+AB=a+b��
��2���ٸ��ݵȱ�������ABD�͵ȱ�������ACE���ɵ���CAD�ա�EAB��SAS��������ȫ�������ε����ʿɵ�CD=BE��
�ڸ���ȫ�������ε����ʿɵã��߶�BE�������ֵ=�߶�CD�������ֵ�������߶�CD�ij�ȡ�����ֵʱ����D��CB���ӳ����ϣ���ʱCD=3+1=4���ɵ�BE=4��
�����������1����ͼ1��

�ߵ�AΪ�߶�BC��һ���㣬��BC=a��AB=b��
�൱��Aλ��CB���ӳ�����ʱ���߶�AC�ij�ȡ�����ֵ�������ֵΪBC+AB=a+b��
��2����CD=BE��
���ɣ���ͼ2��
��������ABD��������ACE�ǵȱ���������
��AD=AB��AC=AE����BAD=��CAE=60����
���BAD+��BAC=��CAE+��BAC��
����CAD=��EAB��
����CAD����EAB��

���CAD�ա�EAB��SAS����
��CD=BE��
���߶�BE�������ֵΪ4��
���ɣ����߶�BE�������ֵ=�߶�CD�������ֵ��
�൱�߶�CD�ij�ȡ�����ֵʱ����D��CB���ӳ����ϣ�
��ʱCD=3+1=4��
��BE=4��



