题目内容
解方程、解不等式组,并将其解集在数轴上表示出来.
(1)
+
=2
(2)
.
(1)
| x |
| 2x-1 |
| 11 |
| 1-2x |
(2)
|
分析:(1)方程两边都乘以最简公分母(2x-1)把分式方程化为整式方程,求解然后进行检验;
(2)先求出两个不等式的解集,再求其公共解.
(2)先求出两个不等式的解集,再求其公共解.
解答:解:(1)方程两边都乘以(2x-1)得,
x-11=4x-2,
解得x=-3,
检验:当x=-3时,2x-1=2×(-3)-1=-7≠0,
所以原分式方程的解是x=-3;
(2)
,
解不等式①得,x≥-3,
解不等式②得,x<1,
在数轴上表示如下:
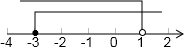
所以不等式组的解集是-3≤x<1.
x-11=4x-2,
解得x=-3,
检验:当x=-3时,2x-1=2×(-3)-1=-7≠0,
所以原分式方程的解是x=-3;
(2)
|
解不等式①得,x≥-3,
解不等式②得,x<1,
在数轴上表示如下:

所以不等式组的解集是-3≤x<1.
点评:(1)考查了解分式方程,①解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.②解分式方程一定注意要验根.
(2)考查了一元一次不等式组的解法,在数轴上表示不等式组的解集,需要把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
(2)考查了一元一次不等式组的解法,在数轴上表示不等式组的解集,需要把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目