题目内容
设m是实数，那么平面上的点P（3m2-5m+2，1-m）不可能在第几象限？
解：∵3m2-5m+2=（m-1）（3m-2），
∴当m≤
时，3m2-5m+2≥0，
此时1-m＞0，点P在第一象限或y轴上；
当＜m＜1时，3m2-5m+2＜0，
此时1-m＞0，点P在第二象限；
当m≥1时，3m2-5m+2≥0，此时1-m≤0，点P在第四象限或坐标原点．
综合以上结论可知，点P不可能在第三象限．
分析：根据各象限内点的特点，进行逐一分析即可求解．
点评：本题综合性较强，考查了象限内点的符号特点与因式分解，以及学生的逻辑推理能力．
∴当m≤
时，3m2-5m+2≥0，此时1-m＞0，点P在第一象限或y轴上；
当
＜m＜1时，3m2-5m+2＜0，此时1-m＞0，点P在第二象限；
当m≥1时，3m2-5m+2≥0，此时1-m≤0，点P在第四象限或坐标原点．
综合以上结论可知，点P不可能在第三象限．
分析：根据各象限内点的特点，进行逐一分析即可求解．
点评：本题综合性较强，考查了象限内点的符号特点与因式分解，以及学生的逻辑推理能力．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
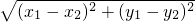．例如：若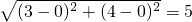
．
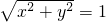，即x2+y2=1成立；反过来，如果点P（x，y）的坐标满足等式x2+y2=1，那么点P必在⊙O上，这时，我们就把等式x2+y2=1称为⊙O的方程．
．
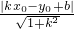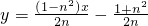的距离．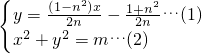
，其中n≠0，m＞0．
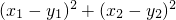是与n无关的常数，并求出这个常数．