题目内容
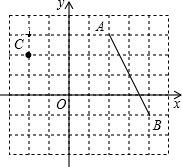 如图,在7×8网格中,每个小正方形的边长均匀为1,线段AB的端点和点C都在网格的格点上,以网格的两条格线建立直角坐标系,原点为O.
如图,在7×8网格中,每个小正方形的边长均匀为1,线段AB的端点和点C都在网格的格点上,以网格的两条格线建立直角坐标系,原点为O.
(1)平移线段AB到线段CD,使点C与点A对应,画出线段CD;
(2)写出∠OAC、∠OBD、∠AOB满足的关系式,并说明理由.
 解:(1)如图所示,D(0,-2);
解:(1)如图所示,D(0,-2);(2)∠AOB=∠OAC+∠OBD.理由如下:
连接AC、BD、OA、OB,
∵线段CD由线段AB平移而成,
∴AC∥BD,
过点O作OE∥AC,
∵AC∥BD,OE∥AC,
∴OE∥BD,
∴∠OAC=∠EOA,∠OBD=∠EOB,
∴∠AOB=∠AOE+∠BOE=∠OAC+∠OBD.
分析:(1)根据图形平移的性质画出线段CD,得出C点坐标即可;
(2)连接AC、BD、OA、OB,由平移的性质可知,AC∥BD,过点O作OE∥AC,根据平行线的传递性可知OE∥AC,由平行线的性质即可得出结论.
点评:本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
 21、如图,在网格中有一个四边形和两个三角形.
21、如图,在网格中有一个四边形和两个三角形. 如图,在6×8网格中,点O和△ABC的顶点均在小正方形的顶点,以O为位似中心,在网格中作△A′B′C′和△ABC位似,且位似比为1:2.
如图,在6×8网格中,点O和△ABC的顶点均在小正方形的顶点,以O为位似中心,在网格中作△A′B′C′和△ABC位似,且位似比为1:2.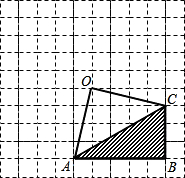 如图,在网格中有一个四边形图案OABC.
如图,在网格中有一个四边形图案OABC.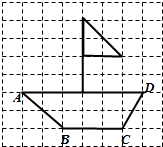 如图,在网格中,有一只小船,点A、B、C、D均在格点上,请按照要求完成任务.
如图,在网格中,有一只小船,点A、B、C、D均在格点上,请按照要求完成任务. 如图,在7×8网格中,每个小正方形的边长均匀为1,线段AB的端点和点C都在网格的格点上,以网格的两条格线建立直角坐标系,原点为O.
如图,在7×8网格中,每个小正方形的边长均匀为1,线段AB的端点和点C都在网格的格点上,以网格的两条格线建立直角坐标系,原点为O.