题目内容
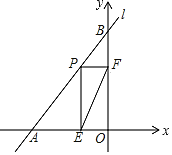
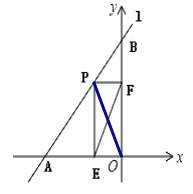
【题目】如图,一次函数y=![]() ,的图象向下平移2个单位后得直线l,直线l交x轴于点A、交y轴于点B,在线段AB上有一动点P(不与点A、B重合),过点P分别作PE⊥x轴点E,PF⊥y轴于点F,当线段EF的长最小时,点P的坐标为_____.
,的图象向下平移2个单位后得直线l,直线l交x轴于点A、交y轴于点B,在线段AB上有一动点P(不与点A、B重合),过点P分别作PE⊥x轴点E,PF⊥y轴于点F,当线段EF的长最小时,点P的坐标为_____.
【答案】(-![]() )
)
【解析】
一次函数![]() ,的图象向下平移2个单位后得直线
,的图象向下平移2个单位后得直线![]() 在一次函数
在一次函数![]() 中,分别令x=0和y=0,解相应方程,可求得A、B两点的坐标,由矩形的性质可知EF=OP,可知当OP最小时,则EF有最小值,由垂线段最短可知当OP⊥AB时,EF最小,由此可知P点坐标.
中,分别令x=0和y=0,解相应方程,可求得A、B两点的坐标,由矩形的性质可知EF=OP,可知当OP最小时,则EF有最小值,由垂线段最短可知当OP⊥AB时,EF最小,由此可知P点坐标.
一次函数![]() ,的图象向下平移2个单位后得直线
,的图象向下平移2个单位后得直线![]() ,
,
由矩形的性质可知EF=OP,由垂线段最短可知当OP⊥AB时,则EF有最小值,
设P点的坐标(x,![]() ),
),
x=0和y=0,解相应方程A(-![]() ),B(
),B(![]() ),
),
AO=BO,
又OP⊥AB,
AP=BP,P为中点,
PE⊥![]() 轴点,PF⊥
轴点,PF⊥![]() 轴,
轴,
PF平行等于![]() AO,PE平行等于
AO,PE平行等于![]() BO,
BO,
PE=PF=![]() ,
,
此时EF最小,可知P点坐标(-![]() ).
).

练习册系列答案
相关题目
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.