题目内容
如图,点A是直线y=-2x+3上的动点,过点A作AB垂直x轴于点B,y轴上存在点C,能使以A、B、C为顶点的三角形是等腰直角三角形.请写出所有符合条件的点C的坐标______.
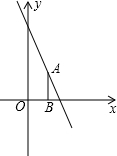

以A、B、C为顶点的等腰直角三角形分为以A为直角顶点,以B为直角顶点,以C为直角顶点三种情况.
设A(x,y),B(x,0),C(0,c),
(1)以A为直角顶点,则AB、AC为等腰的两条边,
∴若y=x=c.
由A在直线y=-2x+3得:x=-2x+3
∴x=1,y=1故得C(0,1).
若y=-x=c的情况,
∴-x=-2x+3,解得x=3,
C的坐标为(0,-3)
(2)以B为直角,则AB,BC为等腰的两条边,
∴C(0,0).
(3)以C为直角,则AC,BC为等腰的两条边,
此时y2=2×(x2+c2),(y-c)2+x2=x2+c2,
又y=-2x+3,
∴联立解得:c=
故得C(0,
).
综上所诉:C的所有可能值为(0,1)(0,0)(0,-3)(0,
).
设A(x,y),B(x,0),C(0,c),
(1)以A为直角顶点,则AB、AC为等腰的两条边,
∴若y=x=c.
由A在直线y=-2x+3得:x=-2x+3
∴x=1,y=1故得C(0,1).
若y=-x=c的情况,
∴-x=-2x+3,解得x=3,
C的坐标为(0,-3)
(2)以B为直角,则AB,BC为等腰的两条边,
∴C(0,0).
(3)以C为直角,则AC,BC为等腰的两条边,
此时y2=2×(x2+c2),(y-c)2+x2=x2+c2,
又y=-2x+3,
∴联立解得:c=
| 3 |
| 4 |
故得C(0,
| 3 |
| 4 |
综上所诉:C的所有可能值为(0,1)(0,0)(0,-3)(0,
| 3 |
| 4 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目