题目内容
【题目】如图![]() ,点
,点![]() 将线段
将线段![]() 分成两部分,如果
分成两部分,如果![]() ,那么称点
,那么称点![]() 为线段
为线段![]() 的黄金分割点,某教学兴趣小组在进行研究时,由“黄金分割点”联想到“黄金分割线”,类似的给出“黄金分割线”的定义:“一直线将一个面积为
的黄金分割点,某教学兴趣小组在进行研究时,由“黄金分割点”联想到“黄金分割线”,类似的给出“黄金分割线”的定义:“一直线将一个面积为![]() 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为![]() ,
,![]() ,如果
,如果![]() ,那么称这条直线为该图形的黄金分割线.
,那么称这条直线为该图形的黄金分割线.
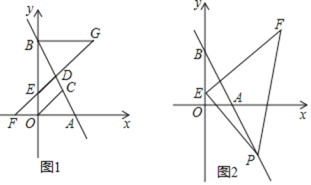
![]() 如图
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,请问直线
,请问直线![]() 是不是
是不是![]() 的黄金分割线,并证明你的结论;
的黄金分割线,并证明你的结论;
![]() 如图
如图![]() ,在边长为
,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 是边
是边![]() 上一点,若直线
上一点,若直线![]() 是正方形
是正方形![]() 的黄金分割线,求
的黄金分割线,求![]() 的长.
的长.
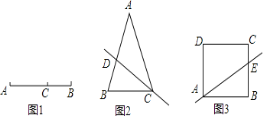
【答案】![]() 直线
直线![]() 是
是![]() 的黄金分割线,理由见解析;(2)
的黄金分割线,理由见解析;(2)![]() 长为
长为![]() .
.
【解析】
(1)如图2,根据等高三角形的面积比等于底的比可得![]() ,
,![]() ,
,
要证直线CD是△ABC的黄金分割线,只需证![]() ,只需证
,只需证![]() ,易证BC=AD,只需证
,易证BC=AD,只需证![]() ,只需证△BCD∽△BAC即可;
,只需证△BCD∽△BAC即可;
(2)设BE=x,如图3,易得![]() ,
,![]() ,
,![]() .由直线AE是正方形ABCD的黄金分割线可得
.由直线AE是正方形ABCD的黄金分割线可得![]() ,由此得到关于x的方程,解这个方程就可解决问题.
,由此得到关于x的方程,解这个方程就可解决问题.
解:![]() 直线
直线![]() 是
是![]() 的黄金分割线.
的黄金分割线.
理由:如图![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,

∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴直线![]() 是
是![]() 的黄金分割线;
的黄金分割线;
![]() 设
设![]() ,如图
,如图![]() ,
,
∵正方形![]() 的边长为
的边长为![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵直线![]() 是正方形
是正方形![]() 的黄金分割线,
的黄金分割线,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
解得:![]() ,
,![]() .
.
∵点![]() 是边
是边![]() 上一点,
上一点,
∴![]() ,
,
∴![]() ,
,
∴![]() 长为
长为![]() .
.

练习册系列答案
相关题目