题目内容
 如图所示,点D、E分别是AB、AC的中点,点F、G分别为BD、CE的中点,若FG=6,则DE+BC=
如图所示,点D、E分别是AB、AC的中点,点F、G分别为BD、CE的中点,若FG=6,则DE+BC=分析:根据中位线定理得:DE=
BC,根据梯形中位线定理得FG=
(DE+BC),由FG=6求得DE+BC的值即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵点F、G分别为BD、CE的中点,
∴FG=
(DE+BC),
∵FG=6,
∴DE+BC=2FG=2×6=12;
∵D、E分别是AB、AC的中点,
∴DE=
BC,
∴DE+BC=
BC+BC=
BC=12,
∴BC=8.
故答案为:12;8.
∴FG=
| 1 |
| 2 |
∵FG=6,
∴DE+BC=2FG=2×6=12;
∵D、E分别是AB、AC的中点,
∴DE=
| 1 |
| 2 |
∴DE+BC=
| 1 |
| 2 |
| 3 |
| 2 |
∴BC=8.
故答案为:12;8.
点评:本题考查了梯形的中位线与三角形的中位线的性质,是一道不错的几何综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
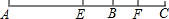
 3、如图所示,点M,N分别是正八边形相邻两边AB,BC上的点,且AM=BN,则∠MON=
3、如图所示,点M,N分别是正八边形相邻两边AB,BC上的点,且AM=BN,则∠MON=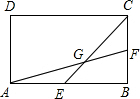 如图所示,点E,F分别是矩形ABCD的边AB,BC的中点,连接AF,EC交于点G,则
如图所示,点E,F分别是矩形ABCD的边AB,BC的中点,连接AF,EC交于点G,则