题目内容
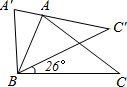 如图,把△ABC绕B点逆时针方旋转26°得到△A′BC′,若A′C′正好经过A点,则∠BAC=
如图,把△ABC绕B点逆时针方旋转26°得到△A′BC′,若A′C′正好经过A点,则∠BAC=
- A.52°
- B.64°
- C.77°
- D.82°
C
分析:根据旋转的性质,易得∠ABA′=∠CBC′=∠CAC′=26°且AB=A′B,进而可得∠A′AB=77°,代入数据计算可得∠BAC的大小.
解答:根据题意:∵△ABC绕B点逆时针方旋转26°得到△A′BC′,且A′C′正好经过A点,
∴∠ABA′=∠CBC′=∠CAC′=26°,AB=A′B,
∴∠A′AB=77°,∠BAC=180-26-77=77°.
故选C.
点评:本题考查旋转两相等的性质,即对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.
分析:根据旋转的性质,易得∠ABA′=∠CBC′=∠CAC′=26°且AB=A′B,进而可得∠A′AB=77°,代入数据计算可得∠BAC的大小.
解答:根据题意:∵△ABC绕B点逆时针方旋转26°得到△A′BC′,且A′C′正好经过A点,
∴∠ABA′=∠CBC′=∠CAC′=26°,AB=A′B,
∴∠A′AB=77°,∠BAC=180-26-77=77°.
故选C.
点评:本题考查旋转两相等的性质,即对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
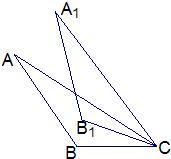 14、如图,把△ABC绕点C顺时针旋转22度,得△A1B1C,则直线AB与A1B1所成的锐角为
14、如图,把△ABC绕点C顺时针旋转22度,得△A1B1C,则直线AB与A1B1所成的锐角为
 (2013•沁阳市一模)如图,把△ABC绕着点C顺时针旋转30°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A的度数是( )
(2013•沁阳市一模)如图,把△ABC绕着点C顺时针旋转30°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A的度数是( )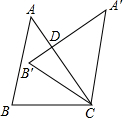 如图,把△ABC绕点C顺时针旋转43°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A=
如图,把△ABC绕点C顺时针旋转43°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A=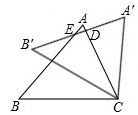 如图,把△ABC绕点C顺时针旋转25°,得到△A′B′C′,A′B′分别交AC、AB于点D、E,若∠A′DC=80°,则∠A=
如图,把△ABC绕点C顺时针旋转25°,得到△A′B′C′,A′B′分别交AC、AB于点D、E,若∠A′DC=80°,则∠A=