题目内容
(2012•南关区模拟)如图,矩形ABCO(OA>OC)的两边分别在x轴的负半轴和y轴的正半轴上,点B在反比例函数y=-
(x<0)的图象上,且OC=2.将矩形ABCO以C为旋转中心,逆时针转90°后得到矩形EFCD,反比例函数y=
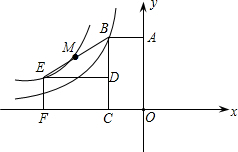 (x<0)的图象经过点E.
(x<0)的图象经过点E.
(1)求k的值;
(2)判断线段BE的中点M是否在反比例函数y=
(x<0)的图象上,请说明理由.
| 8 |
| x |
| k |
| x |
 (x<0)的图象经过点E.
(x<0)的图象经过点E.(1)求k的值;
(2)判断线段BE的中点M是否在反比例函数y=
| k |
| x |
分析:(1)首先根据反比例函数y=-
且OC=2可得到B点坐标,再根据旋转的方法可得到E点坐标,再根据反比例函数图象上点的坐标特点可算出k的值;
(2)首先根据B、E两点坐标可得到BE的中点坐标,再根据反比例函数图象上点的坐标特点可判断出点M是否在反比例函数y=
(x<0)的图象上.
| 8 |
| x |
(2)首先根据B、E两点坐标可得到BE的中点坐标,再根据反比例函数图象上点的坐标特点可判断出点M是否在反比例函数y=
| k |
| x |
解答:解:(1)∵点B在反比例函数y=-
(x<0)的图象上,且OC=2,
∴B(-2,4),
∴OA=4,
∵将矩形ABCO以C为旋转中心,逆时针转90°后得到矩形EFCD,
∴E(-6,2).
∵反比例函数y=
(x<0)的图象经过点E,
∴k=-6×2=-12;
(2)∵B(-2,4),E(-6,2),
∴M(-4,3),
∵-4×3=-12,
∴线段BE的中点M在反比例函数y=-
(x<0)的图象上.
| 8 |
| x |
∴B(-2,4),
∴OA=4,
∵将矩形ABCO以C为旋转中心,逆时针转90°后得到矩形EFCD,
∴E(-6,2).
∵反比例函数y=
| k |
| x |
∴k=-6×2=-12;
(2)∵B(-2,4),E(-6,2),
∴M(-4,3),
∵-4×3=-12,
∴线段BE的中点M在反比例函数y=-
| 12 |
| x |
点评:此题主要考查了反比例函数的综合应用,关键是掌握凡是反比例函数图象上的点,横纵坐标的积=k.

练习册系列答案
相关题目
 (2012•南关区模拟)如图,半径为1的动圆P圆心在抛物线y=(x-2)2-1上,当⊙P与x轴相切时,点P的坐标为
(2012•南关区模拟)如图,半径为1的动圆P圆心在抛物线y=(x-2)2-1上,当⊙P与x轴相切时,点P的坐标为