题目内容
已知动点P以每秒2cm的速度沿如图所示的边框按从B?C?D?E?F?A的路径移动,相应的△ABP的面积S关于时间t的函数图象如图所示,若AB=6cm,试回答下列问题:
(1)动点P在线段 上运动的过程中△ABP的面积S保持不变.
(2)BC= cm; CD= cm; DE= cm; EF= cm
(3)求出图乙中的a与b的值.
(1) CD和EF;(2) 8cm; 4cm ; 6cm; 2 cm;(3)a=24,b=17
解析试题分析:(1)利用底高相同,面积相等可知点P在CD和EF上△ABP的面积S保持不变;
(2)先根据△ABC的面积为24cm2,AB=6cm,求出BC的长度,再由动点P在BC上运动的时间是4秒,即可求出动点的速度v;由动点P在CD上移动的时间为2秒及速度v,即可求出线段CD的长度,同理,由动点P在DE上移动的时间为3秒及(1)中求出的动点的速度v,即可求出线段DE的长度;
(3)当t=9秒时,动点P移动到点E,则a=S= AB•(BC+DE),代入数值即可求解;计算BC+CD+DE+EF+FA的长度,又由动点P的速度,计算可得b的值.
AB•(BC+DE),代入数值即可求解;计算BC+CD+DE+EF+FA的长度,又由动点P的速度,计算可得b的值.
试题解析:(1)根据题意知:点P在CD和EF上△ABP的面积S保持不变;
(2)由图可知,当点P在BC上移动时,△PAB可看作以AB为底、BP为高,则它的面积S随BP的增大而增大,当点P到达点C时面积达到最大值24,
∵S△ABC=24,
∴ ×6×BC=24,
×6×BC=24,
∴BC=8(cm),
又∵点P在BC上移动了4秒,
∴BC=4v,
∴4v=8,
∴v=2(cm/s);
当点P在CD上移动时,底边AB不变,高不变,因而面积不变,恒为24,由图象可知
点P移动的时间为6-4=2(s),
则CD=2×2=4(cm).
当点P在DE上移动时,△PAB可看作以AB为底、BP为高,则它的面积S随BP的增大而增大,当点P到达点E时面积达到最大值a,
∵点P在DE上移动了9-6=3(s),
∴DE=3×2=6(cm);
EF=AB-CD=6-4=2cm.
(3)∵点P移动到点E时面积达到最大值a,
∴a= AB•(BC+DE),
AB•(BC+DE),
∵AB=6cm,BC=8cm,DE=6cm,
∴a= ×6×(8+6)=42(cm2).
×6×(8+6)=42(cm2).
∵FA=BC+DE=8+6=14(cm),CD+EF=AB=6cm,
∴BC+CD+DE+EF+FA=(BC+DE)+(CD+EF)+FA=14+6+14=34(cm),
∴b=34÷2="17" (s).
考点:动点问题的函数图象.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案已知一次函数y=kx+b的图象如图所示,则k、b的符号是( )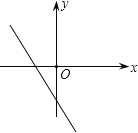
| A.k<0,b<0 | B.k>0,b<0 | C.k<0,b>0 | D.k>0,b>0 |
一次函数y=2x﹣3的图象不经过( )
| A.第一象限&nbs, | B.第二象限&nbs, | C.第三象限&nbs, | D.第四象限&nbs, |
下列说法错误的是( )
| A.抛物线y=﹣x2+x的开口向下 |
| B.两点之间线段最短 |
| C.角平分线上的点到角两边的距离相等 |
| D.一次函数y=﹣x+1的函数值随自变量的增大而增大 |
 的解为 .
的解为 . .
. .
. ,
, ,0)
,0)
 与月份
与月份 的函数关系式是
的函数关系式是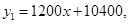 小张1~6月份的销售额
小张1~6月份的销售额 也是月份
也是月份