题目内容
【题目】正方形纸片ABCD的对称中心为O,翻折∠A使顶点A重合于对角线AC上一点P,EF是折痕:
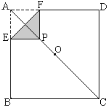
(1)证明:AE=AF;
(2)尺规作图:在图中作出当点P是OC中点时的△EFP(不写画法,保留作图痕迹);完成作图后,标注所作△EFP的外接圆心M.
【答案】(1)、证明过程见解析;(2)、答案见解析.
【解析】
试题分析:(1)、设AP交EF于点Q,根据P是A的对称点得出AP⊥EF,从而得出△AEQ和△AFQ全等,从而得到AE=AF;(2)、根据外接圆的圆心画法得出答案.
试题解析:(1)、设AP交EF于点Q,∵P是A的对称点, ∴AP⊥EF,
在△AEQ和△AFQ中:∵点P在AC上,∴∠EAQ=∠FAQ=45°AQ公共边,∠AQE=∠AQF=90°
∴△AEQ≌△AFQ(ASA)∴AE=AF
(2)、尺规作图:OC中点P
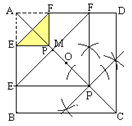
作AP垂直平分线EF、 或PE、PF用角平分线、或过P作垂直线等方法获得△EFP
△EFP的外接圆心M的位置是EF与AC的交点

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
