题目内容
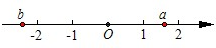 已知a,b两数在数轴上表示如图,化简:
已知a,b两数在数轴上表示如图,化简:| (a+2)2 |
| (b-2)2 |
| (a+b)2 |
分析:根据数轴可以得到:b<-2<1<a<2,则根据加法法则可以得到a+2>0,b-2<0,a+b<0,然后根据绝对值的性质:正数的绝对值是它的本身,负数的绝对值是它的相反数,0的绝对值是0,即可去掉绝对值符号,然后合并同类项即可.
解答:解:根据数轴可以得到:b<-2<1<a<2,
则a+2>0,b-2<0,a+b<0,
∴原式=a+2-(2-b)-(a+b)
=a+2-2+b-a-b
=0.
则a+2>0,b-2<0,a+b<0,
∴原式=a+2-(2-b)-(a+b)
=a+2-2+b-a-b
=0.
点评:本题考查了绝对值的性质,以及加法法则,正确确定a+2>0,b-2<0,a+b<0是关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )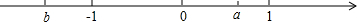
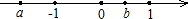 已知 a、b两数在数轴上对应的点如图所示,下列结论正确的是( )
已知 a、b两数在数轴上对应的点如图所示,下列结论正确的是( ) 已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )
已知a,b两数在数轴上对应的点如图所示,下列结论正确的是( )