题目内容
在数学中,为了简便,记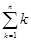 =1+2+3+…+(n-1)+ n.
=1+2+3+…+(n-1)+ n.
1!=1,2!=2×1,3!=3×2×1,…,n!=n×(n-1)×(n-2)×…×3×2×1.
则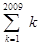 -
-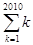 +
+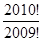 = .
= .
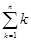 =1+2+3+…+(n-1)+ n.
=1+2+3+…+(n-1)+ n.1!=1,2!=2×1,3!=3×2×1,…,n!=n×(n-1)×(n-2)×…×3×2×1.
则
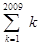 -
-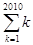 +
+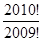 = .
= .0
试题考查知识点:
思路分析:
具体解答过程:
∵
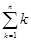 =1+2+3+…+(n-1)+ n
=1+2+3+…+(n-1)+ n∴
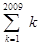 =1+2+3+…+2008+ 2009,
=1+2+3+…+2008+ 2009,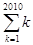 =1+2+3+…+2009+2010
=1+2+3+…+2009+2010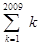 -
-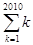 =(1+2+3+…+2008+ 2009)-(1+2+3+…+2009+2010)=-2010
=(1+2+3+…+2008+ 2009)-(1+2+3+…+2009+2010)=-2010∵n!=n×(n-1)×(n-2)×…×3×2×1
∴
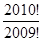 =
=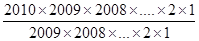 =2010
=2010∴
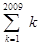 -
-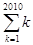 +
+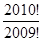 =-2010+2010=0
=-2010+2010=0试题点评:既要考虑新规则,又必须考虑老规则。

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
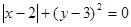 ,则
,则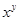 的值为( )
的值为( )



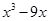 =__________。
=__________。 .
. ,X*2定义为X*2=
,X*2定义为X*2= ,则多项式
,则多项式 ( X*2)
( X*2) 在x=2时的值为( ).
在x=2时的值为( ).


 ,
, ,则
,则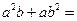 .
.