题目内容
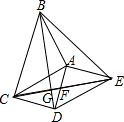 如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交 CE于点G,连接BE.下列结论中:①CE=BD; ②△ADC是等腰三角形;
如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交 CE于点G,连接BE.下列结论中:①CE=BD; ②△ADC是等腰三角形;
③∠CGD+∠DAE=180°; ④CD•AE=EF•CG.一定正确的结论有
- A.1个
- B.2个
- C.3个
- D.4个
D
分析:①利用SAS证明△BAD≌△CAE,可得到CE=BD;
②利用平行四边形的性质可得AE=CD,再结合△ADE是等腰直角三角形可得到△ADC是等腰直角三角形;
③利用△BAD≌△CAE,△BAE≌△BAD,得出△CAE≌△BAE,可得到∠CGD+∠DAE=180°;
④利用得出∠GFD=∠AFE,以及∠GDF+GFD=90°,进而得出△CGD∽△EAF,得出比例式.
解答:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即:∠BAD=∠CAE,
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AE=AD,
∴△BAD≌△CAE(SAS),
∴CE=BD,
∴故①正确;
②∵四边形ACDE是平行四边形,
∴∠EAD=∠ADC=90°,AE=CD,
∵△ADE都是等腰直角三角形,
∴AE=AD,
∴AD=CD,
∴△ADC是等腰直角三角形,
∴②正确;
④∵△BAD≌△CAE,△BAE≌△BAD,
∴△CAE≌△BAE,
∴∠BEA=∠AEC=∠BDA,
∵∠AEF+∠AFE=90°,
∴∠AFE+∠BEA=90°,
∵∠GFD=∠AFE,
∴∠GDF+GFD=90°,
∴∠CGD=90°,
∵∠FAE=90°,∠GCD=∠AEF,
∴△CGD∽△EAF,
∴ ,
,
∴CD•AE=EF•CG.
故④正确,
③由④得∵∠CGD=90°,∠DAE=90°,
∴③∠CGD+∠DAE=180°
故③正确;
故正确的有4个.
故选D.
点评:此题主要考查了全等三角形的判定及性质,以及相似三角形的判定,注意细心分析,熟练应用全等三角形的判定以及相似三角形的判定是解决问题的关键.
分析:①利用SAS证明△BAD≌△CAE,可得到CE=BD;
②利用平行四边形的性质可得AE=CD,再结合△ADE是等腰直角三角形可得到△ADC是等腰直角三角形;
③利用△BAD≌△CAE,△BAE≌△BAD,得出△CAE≌△BAE,可得到∠CGD+∠DAE=180°;
④利用得出∠GFD=∠AFE,以及∠GDF+GFD=90°,进而得出△CGD∽△EAF,得出比例式.
解答:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即:∠BAD=∠CAE,
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AE=AD,
∴△BAD≌△CAE(SAS),
∴CE=BD,
∴故①正确;
②∵四边形ACDE是平行四边形,
∴∠EAD=∠ADC=90°,AE=CD,
∵△ADE都是等腰直角三角形,

∴AE=AD,
∴AD=CD,
∴△ADC是等腰直角三角形,
∴②正确;
④∵△BAD≌△CAE,△BAE≌△BAD,
∴△CAE≌△BAE,
∴∠BEA=∠AEC=∠BDA,
∵∠AEF+∠AFE=90°,
∴∠AFE+∠BEA=90°,
∵∠GFD=∠AFE,
∴∠GDF+GFD=90°,
∴∠CGD=90°,
∵∠FAE=90°,∠GCD=∠AEF,
∴△CGD∽△EAF,
∴
 ,
,∴CD•AE=EF•CG.
故④正确,
③由④得∵∠CGD=90°,∠DAE=90°,
∴③∠CGD+∠DAE=180°
故③正确;
故正确的有4个.
故选D.
点评:此题主要考查了全等三角形的判定及性质,以及相似三角形的判定,注意细心分析,熟练应用全等三角形的判定以及相似三角形的判定是解决问题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
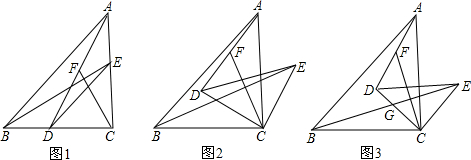
 10、如图,△ABC和△ADE都是等腰直角三角形,∠ACB和∠AED都是直角,点C在AD上,如果△ABC经旋转后能与△ADE重合,那么点
10、如图,△ABC和△ADE都是等腰直角三角形,∠ACB和∠AED都是直角,点C在AD上,如果△ABC经旋转后能与△ADE重合,那么点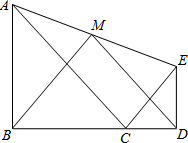 如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,BC=3,CD=1.
如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,BC=3,CD=1.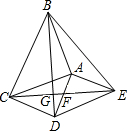 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交 CE于点G,连接BE.下列结论中:
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交 CE于点G,连接BE.下列结论中: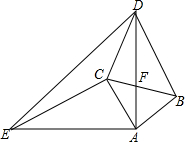 如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.