题目内容
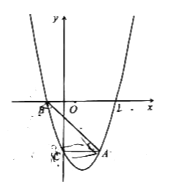
【题目】据统计:超速行驶是引发交通事故的主要原因,学完第一章后,李鹏、王军、张力三位同学尝试用自己所学的知识检测车速,他们决定在峨城大道金源山水城路段进行测试汽车速度的实验,并把观测点设在到公路l的距离为30米的点P处,选择了一辆匀速行驶的大众轿车作为观测对象,测得此车从A处行驶到B处所用的时间为3秒,并测得∠PAO=45°,同时发现将△BPO沿过A点的直线折叠,点B能与点P重合,试判断此车是否超过了每小时60千米的限制速度?并说明理由.
【答案】解:∵由题意得:∠AOP=90°,PO=30m,∠PAO=45°,
∴∠OAP=∠OPA=45°.
∴AO=OP=30.
在Rt△AOP中,由勾股定理可知:AP= ![]() =30
=30 ![]() .
.
∵由翻折的性质可知AB=AP,
∴AB=30 ![]() .
.
∴汽车行驶的速度=30 ![]() ÷3×3.6≈50.76(千米/时).
÷3×3.6≈50.76(千米/时).
∵50.76<60,
∴汽车未超限制速度.
【解析】运用折叠性质可转化AB=AP,再利用勾股定理可求出速度,与60比较大小,得出答案.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目