题目内容
试证明:二次函数y=nx2-2mx-2n的图象与x轴交于不同的A、B两点,并回答下列问题:若二次函数y=nx2-2mx-2n的图象的顶点在以AB为直径的圆上.
(1)m、n间有何关系?
(2)设以AB为直径的圆与y轴交于点C、D,弦CD的长是否为定值?
分析:(1)要证明原抛物线与x轴有两个不同的交点,只要证明当y=0时△>0就可以说明抛物线与x轴有两个不同的交点.然后将抛物线的解析式转化为顶点式,再根据根与系数的关系和两点间的距离公式可以求出m、n之间的数量关系.
(2)利用垂径定理和圆周角定理可以证明三角形相似来证明OD2=AO•OB,根据根与系数的关系可以求出OD的值,从而求出CD的值,判断其为定值.
(2)利用垂径定理和圆周角定理可以证明三角形相似来证明OD2=AO•OB,根据根与系数的关系可以求出OD的值,从而求出CD的值,判断其为定值.
解答:解:令y=0时,则nx2-2mx-2n=0,
∴△=(-2m)2-4n(-2n)
=4m2+8n2
∵n≠0
∴△>0
∴方程nx2-2mx-2n=0有两个不同的实数根x1,x2
∴二次函数y=nx2-2mx-2n的图象与x轴交于不同的交点.
(1)∵y=nx2-2mx-2n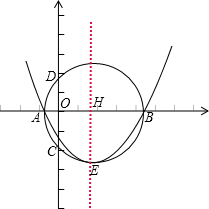
∴y=(x-
)2-2n-
所以它的顶点坐标为(
,-2n-
)
HE=|-2n-
|
∵x1+x2=
,x1•x2=-2
∴AB=|x1-x2|=
=
=
∴
=2|-2n-
|
变形为:m2+2n2=1
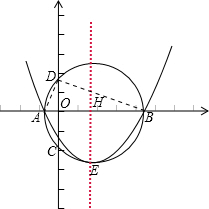
(2)连接AD、BD
∴∠ADB=90°
∴OD2=OA•OB=|x1|•|x2|=|x1x2|=2
∴OD=
∵CD=2OD
∴CD=2
即CD的长为恒值2
.
∴△=(-2m)2-4n(-2n)
=4m2+8n2
∵n≠0
∴△>0
∴方程nx2-2mx-2n=0有两个不同的实数根x1,x2
∴二次函数y=nx2-2mx-2n的图象与x轴交于不同的交点.
(1)∵y=nx2-2mx-2n

∴y=(x-
| m |
| n |
| m2 |
| n |
所以它的顶点坐标为(
| m |
| n |
| m2 |
| n |
HE=|-2n-
| m2 |
| n |
∵x1+x2=
| 2m |
| n |
∴AB=|x1-x2|=
| (x1-x2) 2 |
| (x1+x2)2-4x1x2 |
|
∴
|
| m2 |
| n |
变形为:m2+2n2=1

(2)连接AD、BD
∴∠ADB=90°
∴OD2=OA•OB=|x1|•|x2|=|x1x2|=2
∴OD=
| 2 |
∵CD=2OD
∴CD=2
| 2 |
即CD的长为恒值2
| 2 |
点评:本题是一道二次函数的综合题,考查了二次函数的图象与x轴的交点坐标情况,根与系数的关系及顶点坐标的运用以及定长的问题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
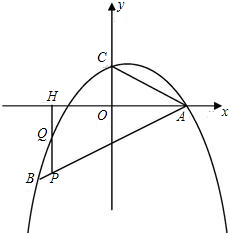 如图,二次函数
如图,二次函数