题目内容
【题目】如图:在三角形ABC中,∠C=90°,AD是三角形ABC的角平分线,AB=AC+CD.
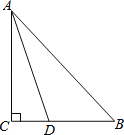
(1)求证:AC=BC;
(2)若BD=![]() ,求AB的长.
,求AB的长.
【答案】(1)见解析;(2)8+4![]() .
.
【解析】
试题分析:(1)作DE⊥AB于E,则∠AED=∠BED=90°,由AAS证明△ADE≌△ADC,得出对应边相等ED=CD,AE=AC,由已知条件得出ED=EB,得出∠B=∠EDB=45°,证出△ABC是等腰直角三角形,即可得出结论;
(2)证出△BDE是等腰直角三角形,得出CD=ED=EB=![]() BD=4,AC=BC=CD+BD=4+4
BD=4,AC=BC=CD+BD=4+4![]() ,即可得出结论.
,即可得出结论.
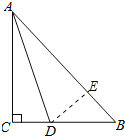
(1)证明:作DE⊥AB于E,则∠AED=∠BED=90°,
∵AD是三角形ABC的角平分线,
∴∠DAE=∠DAC,
在△ADE和△ADC中,
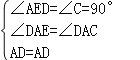 ,
,
∴△ADE≌△ADC(AAS),
∴ED=CD,AE=AC,
∵AB=AC+CD=AE+EB,
∴CD=EB,
∴ED=EB,
∴∠B=∠EDB=45°,
∴∠BAC=45°,
∴△ABC是等腰直角三角形,
∴AC=BC;
(2)解:∵∠B=∠EDB=45°,∠BED=90°,
∴△BDE是等腰直角三角形,
∴CD=ED=EB=![]() BD=4,
BD=4,
∴AC=BC=CD+BD=4+4![]() ,
,
∴AB=AC+CD=4+4![]() +4=8+4
+4=8+4![]() .
.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目