题目内容
【题目】在△ABC中，AB=13cm，AC=20cm，BC边上的高为12cm，则△ABC的面积为cm2 ．
【答案】126或66
【解析】解：当∠B为锐角时（如图1），
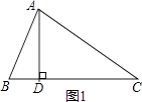
在Rt△ABD中，
BD= 
= 
=5cm，
在Rt△ADC中，
CD= 
= 
=16cm，
∴BC=21，
∴S△ABC= 
= 
×21×12=126cm2；
当∠B为钝角时（如图2），
在Rt△ABD中，
BD= = =5cm，
在Rt△ADC中，
CD= = =16cm，
∴BC=CD﹣BD=16﹣5=11cm，
∴S△ABC= = ×11×12=66cm2，
故答案为：126或66．
分两种情况：当∠B为锐角时，当∠B为钝角时，根据勾股定理得出BD,CD的长，从而得出BC的长，利用面积法求出答案；
练习册系列答案
相关题目
【题目】小明在学习了数据的收集、整理与描述后，为妈妈整理记录了10月份的家庭支出情况，并绘制成如下尚不完整的统计图表，请你根据图表信息完成下列各题：
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | 400 |
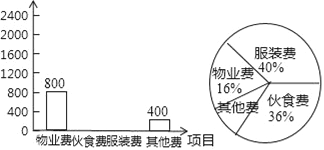
（1）10月份小明家共支出多少元？
（2）在扇形统计图中，表示“其他费”的扇形圆心角为多少度？
（3）请将表格补充完整；
（4）请将条形统计图补充完整．
