题目内容
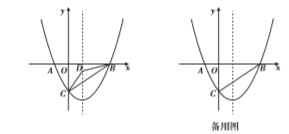
【题目】如图①,在平面直角坐标系中,点A是抛物线y=x2在第一象限上的一个点,连结OA,过点A作AB⊥OA,交y轴于点B,设点A的横坐标为n.
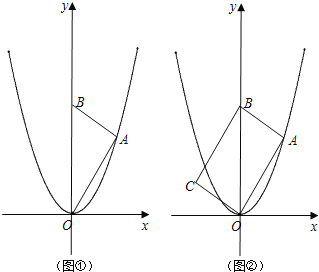
(探究):
(1)当n=1时,点B的纵坐标是 ;
(2)当n=2时,点B的纵坐标是 ;
(3)点B的纵坐标是 (用含n的代数式表示).
(应用):
如图②,将△OAB绕着斜边OB的中点顺时针旋转180°,得到△BCO.
(1)求点C的坐标(用含n的代数式表示);
(2)当点A在抛物线上运动时,点C也随之运动.当1≤n≤5时,线段OC扫过的图形的面积是 .
【答案】探究:(1)2,(2)5,(3) n2+1 应用:(1)(﹣n,1),(2)2.
【解析】
探究;依据直角三角形的射影定理即可求得B点的坐标.
应用:(1)依据全等三角形的性质即可求得C点的坐标,(2)通过(1)可求得C1、C2的坐标,从而得出矩形面积和三角形的面积,最后求得当1≤n≤5时,线段OC扫过的图形的面积.
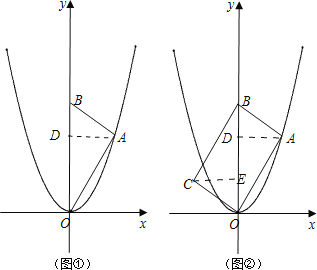
解:探究:如图1所示:设点A的横坐标为n,点A是抛物线y=x2在第一象限上的一个点;
∴A(n,n2);
∴AD=n,OD=n2;
在Rt△ACB中,AD2=ODBD;
设B点的纵坐标为y1,则n2=n2(y1﹣n2),
解得:y1=n2+1,
∴点B的纵坐标是 n2+1.
故(1)n=1时,点B的纵坐标是2
(2)n=2时,点B的纵坐标是5
(3)点B的纵坐标是 n2+1.
应用:(1)点B的纵坐标是 n2+1,A点的纵坐标是n2,
∴BD=1,
根据旋转的定义可知CE=AD=n,OE=BD=1;
∴C点的坐标为:(﹣n,1);
(2)当n=1时C点的坐标为C1(﹣1,1),当n=5时C点的坐标为C2(﹣5,1),
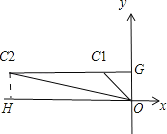
![]()
∴当1≤n≤5时,线段OC扫过的图形的面积是2.

练习册系列答案
相关题目