��Ŀ����
����Ŀ��ֱ��AB��CD����P����ƽ����֮�䣬��E. F�ֱ���AB��CD�ϣ�����PE��PF.����̽�������
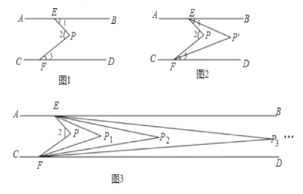
(1)��ͼ1�С�1=36��,��2=63�������3=___��
(2)̽��ͼ1�С�1����2���3֮���������ϵ����˵�����ɣ�
(3)��ͼ2��ʾ,��1���3��ƽ���߽��ڵ�P`,����2=��,�����EP`F�Ķ���(�ú����Ĵ���ʽ��ʾ)��
��4����ͼ3��ʾ,��ͼ2�Ļ�����,����BEP![]() ���DFP
���DFP![]() ��ƽ���߽��ڵ�P
��ƽ���߽��ڵ�P![]() ,��BEP
,��BEP![]() ���DFP
���DFP![]() ��ƽ���߽��ڵ�P
��ƽ���߽��ڵ�P![]() ����BEP
����BEP![]() ���DFP
���DFP![]() ��ƽ���߽��ڵ�P
��ƽ���߽��ڵ�P![]() ,�ҡ�2=��,ֱ��д����EP
,�ҡ�2=��,ֱ��д����EP![]() F�Ķ���(�ú����Ĵ���ʽ��ʾ).
F�Ķ���(�ú����Ĵ���ʽ��ʾ).
���𰸡���1��27������2����2=��1+��3����3��![]() ������4��
������4��![]() ����
����
��������
��1�����ý��ۣ���2=��1+��3���㼴�ɣ�
��2�����ۣ���2=��1+��3����ͼ1�У���PM��AB������ƽ���ߵ�����֤�����ɣ�
��3�����ã�2���н����Լ���ƽ���ߵĶ��弴�ɽ�����⣮
��4��̽�����ɣ����ù��ɽ�����⼴�ɣ�
(1)��3=��2��1=63��36��=27��.
�ʴ�Ϊ27��.
(2)���ۣ���2=��1+��3.
���ɣ���ͼ1��,��PM��AB.
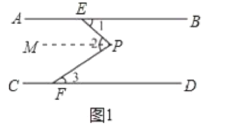
��AB��CD,AB��PM��
��PM��CD��
���1=��MPE����3=��MPF��
���2=��1+��3.
(3)��ͼ2�У�
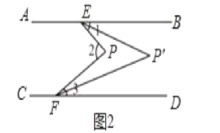
�ߡ�BEP+��DFP=��2=����
���EP��F=��BEP��+��DFP��=![]() (��BEP+��DFP)=
(��BEP+��DFP)=![]() ��.
��.
��4����ͼ3�У�
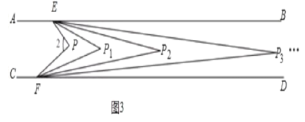
�ɣ�3����֪����P![]() =
=![]() ��,��P
��,��P![]() =(
=(![]() )
)![]() ��,��P
��,��P![]() =(
=(![]() )
)![]() ��,��,��P
��,��,��P![]() =
=![]() ��.
��.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
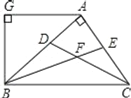
Сѧ��10����Ӧ����ϵ�д�����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ����P�Ӷ���B��������B��C��A��ÿ��1cm���ٶ������˶���A�㣬���˶�ʱ��Ϊx�룬
����P�Ӷ���B��������B��C��A��ÿ��1cm���ٶ������˶���A�㣬���˶�ʱ��Ϊx�룬![]() ����Ϊy cm��ijѧϰС��Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽�������������ǵ�̽�����̣��벹��������
����Ϊy cm��ijѧϰС��Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽�������������ǵ�̽�����̣��벹��������


��1��ͨ��ȡ������ͼ���������õ���x���룩��y��cm���ļ����Ӧֵ��
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
y | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 4.2 | 3.6 | 3.2 | 3.0 | 3.6 | 4.2 | 5.0 |
Ҫ��ȫ�����������ֵ������һλС������
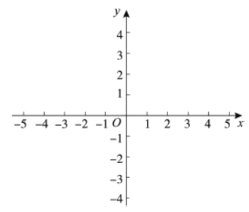
��2����ƽ��ֱ������ϵ�У�����Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
��3����ϻ����ĺ���ͼ������⣺��xԼΪ__________ʱ��![]() ��
��