题目内容
直线y=2x+3与抛物线y=ax2交于A、B两点，已知A点的横坐标是3，求A、B两点的坐标及抛物线的解析式．
解：∵直线y=2x+3与抛物线y=ax2交于A、B两点且A点的横坐标是3，
∴点A的纵坐标y=2×3+3=9，
∴点A的坐标为（3，9），
将点A的坐标代入y=ax2得：a=1，
∴抛物线的解析式为y=x2，
∴
解得：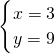
或
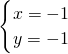
∴点B的坐标为：（-1，1）．
分析：首先根据点A的横坐标求得其纵坐标，然后代入抛物线求得其解析式，然后联立组成方程组后求交点坐标即可．
点评：本题考查了二次函数的性质，重点是知道如何求两图象的交点坐标．
∴点A的纵坐标y=2×3+3=9，
∴点A的坐标为（3，9），
将点A的坐标代入y=ax2得：a=1，
∴抛物线的解析式为y=x2，
∴
解得：
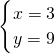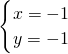
或∴点B的坐标为：（-1，1）．
分析：首先根据点A的横坐标求得其纵坐标，然后代入抛物线求得其解析式，然后联立组成方程组后求交点坐标即可．
点评：本题考查了二次函数的性质，重点是知道如何求两图象的交点坐标．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
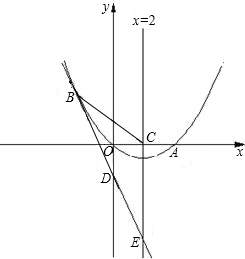（1）求m的值与抛物线的解析式．
如图，已知抛物线y=ax2+bx经过圆点O和x轴上的另一点A，它的对称轴x=2与x轴交于点C，直线y=-2x-1与抛物线y=a2+bx交于点B（-2，m），且y轴、直线x=2分别交于点D、E．