题目内容
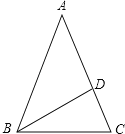
【题目】如图,在△ABC中,BE、CE分别是∠ABC和∠ACB的平分线,过点E作DF∥BC交AB于D,交AC于F,若AB =5,AC =4,则△ADF周长为( ).

A.7B.8C.9D.10
【答案】C
【解析】
根据角平分线的定义可得∠EBD=∠EBC,∠ECF=∠ECB,再根据两直线平行,内错角相等可得∠EBC=∠BED,∠ECB=∠CEF,然后求出∠EBD=∠DEB,∠ECF=∠CEF,再根据等角对等边可得ED=BD,EF=CF,即可得出DF=BD+CF;求出△ADF的周长=AB+AC,然后代入数据进行计算即可得解.
解:∵E是∠ABC,∠ACB平分线的交点,
∴∠EBD=∠EBC,∠ECF=∠ECB,
∵DF∥BC,
∴∠DEB=∠EBC,∠FEC=∠ECB,
∴∠DEB=∠DBE,∠FEC=∠FCE,
∴DE=BD,EF=CF,
∴DF=DE+EF=BD+CF,
即DE=BD+CF,
∴△ADF的周长=AD+DF+AF=(AD+BD)+(CF+AF)=AB+AC,
∵AB=5,AC=4,
∴△ADF的周长=5+4=9,
故选:C.

练习册系列答案
相关题目