题目内容
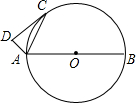已知：如图，DC与⊙O相切于点C，AB为⊙O直径，AD⊥DC于D，∠DCA=28°，则∠CAB的度数是________．
62°
分析：连OC，根据切线的性质得到OC⊥DC，则∠OCD=90°，所以∠ACO=90°-∠DCA=90°-28°=62°，再根据OA=OC即可得到∠CAB的度数．
解答：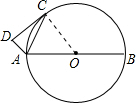
解：连OC，如图，
∵DC与⊙O相切于点C，
∴OC⊥DC，
∴∠OCD=90°，
∵∠DCA=28°，
∴∠ACO=90°-28°=62°，
又∵OC=OA，
∴∠CAB=∠ACO=62°．
故答案为62°．
点评：本题考查了切线的性质：圆的切线垂直于过切点的半径．也考查了等腰三角形的性质．
分析：连OC，根据切线的性质得到OC⊥DC，则∠OCD=90°，所以∠ACO=90°-∠DCA=90°-28°=62°，再根据OA=OC即可得到∠CAB的度数．
解答：
解：连OC，如图，∵DC与⊙O相切于点C，
∴OC⊥DC，
∴∠OCD=90°，
∵∠DCA=28°，
∴∠ACO=90°-28°=62°，
又∵OC=OA，
∴∠CAB=∠ACO=62°．
故答案为62°．
点评：本题考查了切线的性质：圆的切线垂直于过切点的半径．也考查了等腰三角形的性质．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
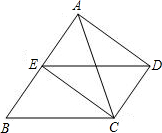已知，如图，DC∥AB，且DC=
已知：如图，DC与⊙O相切于点C，AB为⊙O直径，AD⊥DC于D，∠DCA=28°，则∠CAB的度数是
已知：如图，⊙O与⊙O1交于A和B两点，O在⊙O1上，⊙O的弦BC交⊙O1于D．