题目内容
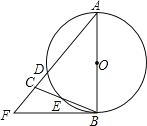
【题目】如图,在△ABC中,AB=AC=10,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠A,tan∠CBF=
∠A,tan∠CBF=![]() ,则CF的长为( )
,则CF的长为( )
A.![]() B.
B.![]()
![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
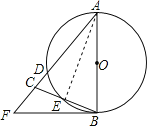
试题分析:连接AE,根据AB是直径,得出AE⊥BC,CE=EB,依据已知条件得出∠CBF=∠EAB,FB是圆的且线,进而得出CB的长,然后根据割线定理求得CD的长,最后根据切割线定理求得FC.
解:连接AE,
∵AB为直径,
∴AE⊥BC,
∵AB=AC,
∴∠EAB=![]() ∠CAB,EB=CE=
∠CAB,EB=CE=![]() CB,
CB,
∵∠CBF=![]() ∠CAB,tan∠CBF=
∠CAB,tan∠CBF=![]() ,
,
∴∠CBF=∠EAB,tan∠EAB=![]() =
=![]() ,
,
∴∠CBF+∠ABC=∠EAB+∠ABC=90°,
∴FB是⊙O的切线,
∴FB2=FDFA,
在RT△AEB中,AB=10,
∴EB=![]() ,
,
∴CB=2![]() ,CE=
,CE=![]() ,
,
∵CECB=CDAC,AC=10,
∴CD=2,
∴AD=AC﹣CD=8,
设CF=x,则FD=x+2,FA=10+x,FB2=AF2﹣AB2=(10+x)2﹣102,
∴(10+x)2﹣102=(x+2)(10+x),
整理得:x=![]() ,
,
∴CF=![]() ,
,
故应选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目