题目内容
【题目】如图,长方形ABCD中,AB=6,BC=8,点P从A出发沿A→B→C→D的路线移动,设点P移动的路线为x,△PAD的面积为y.
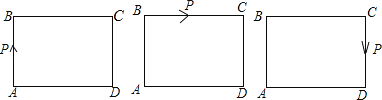
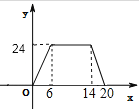
(1)写出y与x之间的函数关系式,并在坐标系中画出这个函数的图象.
(2)求当x=4和x=18时的函数值.
(3)当x取何值时,y=20,并说明此时点P在长方形的哪条边上.
【答案】(1)y与x之间的函数关系式为y=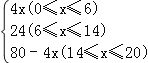 ;
;
(2)当x=4时,y=4x=4×4=16,当x=18时,y=80﹣4x=80﹣4×18=8;
(3)当y=4x=20,解得x=5,此时点P在线段AB上,
当y=80﹣4x=20,解得x=15,此时点P在线段CD上.
【解析】
试题分析:(1)分点P在线段AB上运动时、点P在线段BC上运动时和点P在线段CD上运动时三种情况;
(2)分别将x=4和x=18代入上题求得的函数关系式即可求得其面积;
(3)令y=20,求得x的值,然后根据x的值的大小确定点P的位置即可.
解:(1)当点P在线段AB上时,
此时AP=x,AD=8,
根据三角形的面积公式可得:y=![]() ADAP=
ADAP=![]() ×8×x=4x,
×8×x=4x,
当点P在线段BC上运动时,面积不变;
当点P在线段CD上运动时,
DP=6+8+6﹣x=20﹣x,AD=8
根据三角形的面积公式可得:y=![]() ADDP=
ADDP=![]() ×8×(20﹣x)=80﹣4x,
×8×(20﹣x)=80﹣4x,
∴y与x之间的函数关系式为y=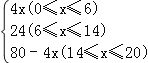
(2)当x=4时,y=4x=4×4=16,
当x=18时,y=80﹣4x=80﹣4×18=8;
(3)当y=4x=20,解得x=5,此时点P在线段AB上,
当y=80﹣4x=20,解得x=15,此时点P在线段CD上.

练习册系列答案
相关题目