��Ŀ����
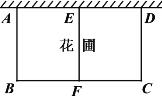
����Ŀ��ѧУҪΧһ�����λ���, ��һ�������㹻����ǽ, �����������Χ��, ��������Ҫ, ��Ҫ��һ����ʽ����Էָ�Ϊ����С���β��֣���ͼ��ʾ��, �ܹ�36�����ǡ�����꣨��������ģ�������δ�ֱ��ǽ���һ��AB�ij�Ϊx�ף�Ҫ��AB��AD��, ���λ���ABCD �����ΪSƽ���ף�
��1����S��![]() ֮��ĺ�����ϵʽ, ��ֱ��д���Ա���
֮��ĺ�����ϵʽ, ��ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��Ҫ��ʹ���λ���ABCD��������, AB�ߵij�ӦΪ�����ף�
���𰸡���1��S=-3x2+36x��0<x<9;��2��ABΪ6��ʱ�����λ���������.
��������
�������ʽ�г����κ������ö��κ���������������ֵ��
��1��![]()
![]()
��2��![]()
���ҽ���![]() ʱ��
ʱ��![]() ȡ���ֵ108��
ȡ���ֵ108��
��ABΪ6��ʱ�����λ���������

��ϰ��ϵ�д�
�����Ŀ