��Ŀ����
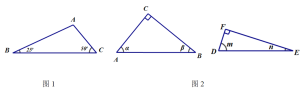
����Ŀ����ͼ���ڳ���Ϊ1����λ���ȵ�С��������ɵ������������У���ABC����������A��B��C���ڸ����.
��1����ͼ1�л�������ABC����ֱ��l����ԳƵ���A1B1C1��
��2����ͼ1��ֱ��l���ҳ�һ��Q,ʹ�� QA+QC1��ֵ��С��
��3����ͼ1��ֱ��l���ҳ�һ��P,ʹ�� |PAPC1| ��ֵ���
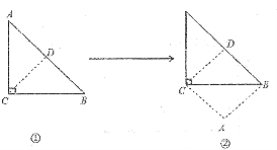
��4����ͼ2�У���һ��![]() ��E��F���ڸ���ϣ�ʹ�߶�BCΪ��BEF�Ľ�ƽ����
��E��F���ڸ���ϣ�ʹ�߶�BCΪ��BEF�Ľ�ƽ����

���𰸡�(1)������;(2)������;(3)������;(4)������.
��������
��1��������Գ�ͼ�ε�������ͼ���ɣ�
��2����������֮���߶���̣�����A1��C1����ֱ��l�Ľ��㼴Ϊ����
��3����������������֮��С�ڵ����ߵ����ʣ���֪����A��C1����ֱ��l�Ľ��㼴Ϊ����;
��4�����ݵ������������ߺ�һ�����ʿ���ͼ.
��ͼ��ʾ��
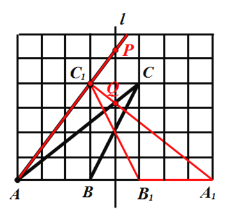
ͼ1
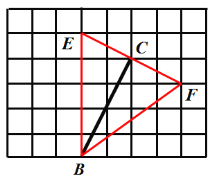
ͼ2

��ϰ��ϵ�д�
 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
�����Ŀ