题目内容
在矩形ABCD中,点O是BC的中点,∠AOD=90°,矩形ABCD的周长为20cm,则AB的长为
- A.1cm
- B.2cm
- C.
 cm
cm - D.
 cm
cm
D
分析:根据矩形性质求出AB=CD,∠B=∠C,可证△ABO≌△DCO,求出∠AOB=∠DOC=45°,求出AB=OB,即可求出答案.
解答:
解:∵O是BC中点.
∴OB=OC,
∵四边形ABCD是矩形,
∴AB=DC,∠B=∠C=90°,
在△ABO和△DCO中
∵ ,
,
∴△ABO≌△DCO(SAS),
∴∠AOB=∠DOC,
∵∠AOD=90°,
∴∠AOB=∠DOC=45°,
∴∠BAO=45°=∠AOB,
∴AB=OB,
∵矩形ABCD的周长是20cm,
∴2(AB+BC)=20cm,
AB+BC=10cm,
∴AB= cm.
cm.
故选D.
点评:本题考查了矩形性质、全等三角形的性质和判定,等腰直角三角形性质的应用,关键是求出AB=OB,题目比较好,难度适中.
分析:根据矩形性质求出AB=CD,∠B=∠C,可证△ABO≌△DCO,求出∠AOB=∠DOC=45°,求出AB=OB,即可求出答案.
解答:

解:∵O是BC中点.
∴OB=OC,
∵四边形ABCD是矩形,
∴AB=DC,∠B=∠C=90°,
在△ABO和△DCO中
∵
 ,
,∴△ABO≌△DCO(SAS),
∴∠AOB=∠DOC,
∵∠AOD=90°,
∴∠AOB=∠DOC=45°,
∴∠BAO=45°=∠AOB,
∴AB=OB,
∵矩形ABCD的周长是20cm,
∴2(AB+BC)=20cm,
AB+BC=10cm,
∴AB=
 cm.
cm.故选D.
点评:本题考查了矩形性质、全等三角形的性质和判定,等腰直角三角形性质的应用,关键是求出AB=OB,题目比较好,难度适中.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
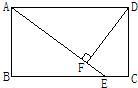 1、如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.线段DF与图中的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明.即DF=
1、如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.线段DF与图中的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明.即DF=AB
.(写出一条线段即可)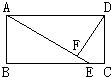 14、如图所示,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE于F,若AB=3,BC=5,则四边形DFEC的面积是( )
14、如图所示,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE于F,若AB=3,BC=5,则四边形DFEC的面积是( )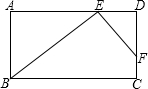
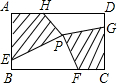 如图,在矩形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,点P在矩形ABCD内,若AB=4,BC=6,AE=CG=3,BF=DH=4,四边形AEPH的面积为5,求四边形PFCG的面积.
如图,在矩形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,点P在矩形ABCD内,若AB=4,BC=6,AE=CG=3,BF=DH=4,四边形AEPH的面积为5,求四边形PFCG的面积.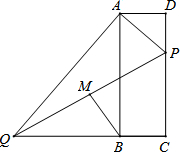 (2013•泰州)如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
(2013•泰州)如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.