题目内容
(2005•金华)如图,在直角坐标系中,点M在y轴的正半轴上,⊙M与x轴交于A,B两点,AD是⊙M的直径,过点D作⊙M的切线,交x轴于点C.已知点A的坐标为(-3,0),点C的坐标为(5,0).(1)求点B的坐标和CD的长;
(2)过点D作DE∥BA,交⊙M于点E,连接AE,求AE的长.
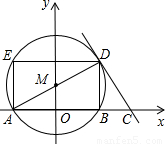
【答案】分析:(1)A点坐标为(-3,0),则B点坐标为(3,0),再根据点C的坐标为(5,0),就可以求出BC与AC的长,根据切割线定理得到CD2=CB•CA,就可以求出CD的长.
(2)根据DE∥BA,得到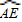 =
=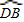 ,所以AE=DB;因而就可以把求AE的问题转化为求BD的问题,在直角△BDC中,根据勾股定理就可以求得.
,所以AE=DB;因而就可以把求AE的问题转化为求BD的问题,在直角△BDC中,根据勾股定理就可以求得.
解答:解:(1)∵MO⊥AB,
∴OA=OB.
∵A点坐标为(-3,0),
∴B点坐标为(3,0);(2分)
∵CD是⊙M的切线,
∴CD2=CB•CA=2×8=16,
∴CD=4.(3分)
(2)∵AD是直径,
∴DB⊥AB,
∴BD= =
= =2
=2 ;(2分)
;(2分)
∵DE∥BA,
∴ =
= ,
,
∴AE=DB,
∴AE=2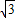 .(2分)
.(2分)
点评:本题主要考查了切割线定理,并且考查了同圆或等圆中相等的弧所对的弦相等.
(2)根据DE∥BA,得到
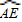 =
=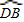 ,所以AE=DB;因而就可以把求AE的问题转化为求BD的问题,在直角△BDC中,根据勾股定理就可以求得.
,所以AE=DB;因而就可以把求AE的问题转化为求BD的问题,在直角△BDC中,根据勾股定理就可以求得.解答:解:(1)∵MO⊥AB,
∴OA=OB.
∵A点坐标为(-3,0),
∴B点坐标为(3,0);(2分)
∵CD是⊙M的切线,
∴CD2=CB•CA=2×8=16,
∴CD=4.(3分)
(2)∵AD是直径,
∴DB⊥AB,
∴BD=
 =
= =2
=2 ;(2分)
;(2分)∵DE∥BA,
∴
 =
= ,
,∴AE=DB,
∴AE=2
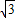 .(2分)
.(2分)点评:本题主要考查了切割线定理,并且考查了同圆或等圆中相等的弧所对的弦相等.

练习册系列答案
相关题目
 .
.
 .
.
 .过D,E两点作直线PQ,与BC边所在的直线MN相交于点F.
.过D,E两点作直线PQ,与BC边所在的直线MN相交于点F.