题目内容
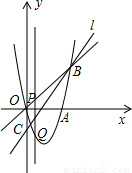
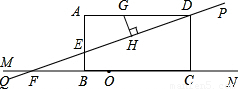
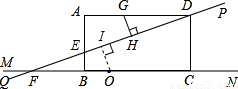
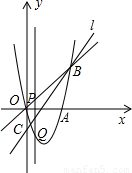
(2005•金华)如图,在矩形ABCD中,AD=8,点E是AB边上的一点,AE=2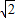 .过D,E两点作直线PQ,与BC边所在的直线MN相交于点F.
.过D,E两点作直线PQ,与BC边所在的直线MN相交于点F.(1)求tan∠ADE的值;
(2)点G是线段AD上的一个动点,GH⊥DE,垂足为H.设DG为x,四边形AEHG的面积为y,试写出y与x之间的函数关系式;
(3)如果AE=2EB,点O是直线MN上的一个动点,以O为圆心作圆,使⊙O与直线PQ相切,同时又与矩形ABCD的某一边相切.问满足条件的⊙O有几个?并求出其中一个圆的半径.
【答案】分析:(1)在Rt△ADE中,已知AD,AE的长,根据三角函数tan∠ADE=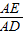 ,代入数据进行求解即可;
,代入数据进行求解即可;
(2)根据y=S△AED-S△DGH,S△AED= AD•AE,S△DGH=
AD•AE,S△DGH= DG•DH•sin∠ADE,故应求sin∠ADE和DH的值;
DG•DH•sin∠ADE,故应求sin∠ADE和DH的值;
在Rt△ADE中,根据勾股定理可将DE的值求出,又知AE的长,故可将sin∠ADH的值求出;
在Rt△DGH中,根据三角函数可将DH的值求出,故将各数据代入进行求解可写出y与x之间的函数关系式;
(3)满足条件的⊙O有4个:⊙O在AB的左侧与AB相切;⊙O在AB的右侧与AB相切;⊙O在CD的左侧与CD相切;⊙O在CD的右侧与CD相切.⊙O在AB的左侧与AB相切为例:作辅助线,过点O作OI⊥FP,垂足为I.根据AD∥FN,得:△AED∽△BEF,可知sin∠PFN,FB的值,在Rt△FOI中,根据sin∠PFN=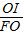 ,可将⊙O的半径求出,其他情况同理可求解半径r.
,可将⊙O的半径求出,其他情况同理可求解半径r.
解答:解:(1)∵矩形ABCD中,∠A=90°,AD=8,AE=2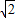 ,
,
∴tan∠ADE= =
=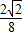 =
= .
.
(2)∵DE=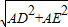 =
=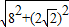 =6
=6 ,
,
∴sin∠ADE=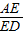 =
=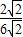 =
= ,cos∠ADE=
,cos∠ADE=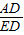 =
=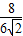 =
=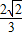 .
.
在Rt△DGH中,
∵GD=x,
∴DH=DG•cos∠ADE=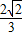 x,
x,
∴S△DGH= DG•DH•sin∠ADE=
DG•DH•sin∠ADE= •x•
•x• x•
x• =
=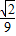 x2.
x2.
∵S△AED= AD•AE=
AD•AE= ×8×2
×8×2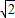 =8
=8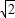 ,
,
∴y=S△AED-S△DGH=8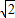 -
-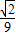 x2,
x2,
即y与x之间的函数关系式是y=-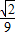 x2+8
x2+8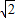 .
.
(3)满足条件的⊙O有4个.
以⊙O在AB的左侧与AB相切为例,求⊙O半径如下:
∵AD∥FN,
∴△AED∽△BEF.
∴∠PFN=∠ADE.
∴sin∠PFN=sin∠ADE= .
.
 ∵AE=2BE,
∵AE=2BE,
∴△AED与△BEF的相似比为2:1,
∴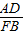 =
= ,FB=4.
,FB=4.
过点O作OI⊥FP,垂足为I,设⊙O的半径为r,那么FO=4-r.
∵sin∠PFN=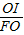 =
=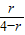 =
= ,
,
∴r=1.
(满足条件的⊙O还有:⊙O在AB的右侧与AB相切,这时r=2;⊙O在CD的左侧与CD相切,这时r=3;⊙O在CD的右侧与CD相切,这时r=6)
点评:本题综合考查了直线与圆的位置关系,解直角三角形,二次函数的应用,三角形相似等多个知识点.
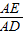 ,代入数据进行求解即可;
,代入数据进行求解即可;(2)根据y=S△AED-S△DGH,S△AED=
 AD•AE,S△DGH=
AD•AE,S△DGH= DG•DH•sin∠ADE,故应求sin∠ADE和DH的值;
DG•DH•sin∠ADE,故应求sin∠ADE和DH的值;在Rt△ADE中,根据勾股定理可将DE的值求出,又知AE的长,故可将sin∠ADH的值求出;
在Rt△DGH中,根据三角函数可将DH的值求出,故将各数据代入进行求解可写出y与x之间的函数关系式;
(3)满足条件的⊙O有4个:⊙O在AB的左侧与AB相切;⊙O在AB的右侧与AB相切;⊙O在CD的左侧与CD相切;⊙O在CD的右侧与CD相切.⊙O在AB的左侧与AB相切为例:作辅助线,过点O作OI⊥FP,垂足为I.根据AD∥FN,得:△AED∽△BEF,可知sin∠PFN,FB的值,在Rt△FOI中,根据sin∠PFN=
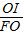 ,可将⊙O的半径求出,其他情况同理可求解半径r.
,可将⊙O的半径求出,其他情况同理可求解半径r.解答:解:(1)∵矩形ABCD中,∠A=90°,AD=8,AE=2
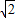 ,
,∴tan∠ADE=
 =
=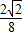 =
= .
.(2)∵DE=
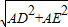 =
=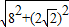 =6
=6 ,
,∴sin∠ADE=
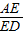 =
=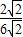 =
= ,cos∠ADE=
,cos∠ADE=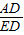 =
=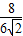 =
=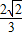 .
.在Rt△DGH中,
∵GD=x,
∴DH=DG•cos∠ADE=
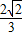 x,
x,∴S△DGH=
 DG•DH•sin∠ADE=
DG•DH•sin∠ADE= •x•
•x• x•
x• =
=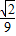 x2.
x2.∵S△AED=
 AD•AE=
AD•AE= ×8×2
×8×2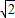 =8
=8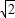 ,
,∴y=S△AED-S△DGH=8
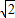 -
-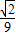 x2,
x2,即y与x之间的函数关系式是y=-
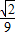 x2+8
x2+8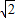 .
.(3)满足条件的⊙O有4个.
以⊙O在AB的左侧与AB相切为例,求⊙O半径如下:
∵AD∥FN,
∴△AED∽△BEF.
∴∠PFN=∠ADE.
∴sin∠PFN=sin∠ADE=
 .
. ∵AE=2BE,
∵AE=2BE,∴△AED与△BEF的相似比为2:1,
∴
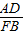 =
= ,FB=4.
,FB=4.过点O作OI⊥FP,垂足为I,设⊙O的半径为r,那么FO=4-r.
∵sin∠PFN=
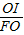 =
=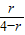 =
= ,
,∴r=1.
(满足条件的⊙O还有:⊙O在AB的右侧与AB相切,这时r=2;⊙O在CD的左侧与CD相切,这时r=3;⊙O在CD的右侧与CD相切,这时r=6)
点评:本题综合考查了直线与圆的位置关系,解直角三角形,二次函数的应用,三角形相似等多个知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.
 .
.