Question

【题目】如图，四边形ABCD是边长为a的正方形，点G、E分别是边AB、BC的中点，∠AEF=90°，且EF交正方形外角的平方线CF于点F．

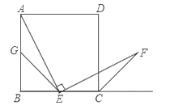
（1）证明：△AGE≌△ECF；（2）求△AEF的面积．

Answer 1

【答案】（1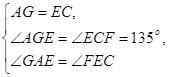）∴△AGE≌△ECF；（2）a2

【解析】

试题（1）证明：∵G，E分别是正方形ABCD的边AB，BC的中点，

∴AG=GB=BE=EC，且∠AGE=180°－45°=135°．

又∵CF是∠DCH的平分线，

∠ECF=90°+45°=135°．

在△AGE和△ECF中，

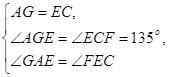
∴△AGE≌△ECF；

（2）解：由△AGE≌△ECF，得AE=EF．

又∵∠AEF=90°，

∴△AEF是等腰直角三角形．

由AB=a，BE=a，知AE=a，

∴S△AEF=a2．