题目内容
【题目】在△ABC中,AB=6,AC=8,则BC边上中线AD的取值范围为( ) (提示:可以构造平行四边形)
A.2<AD<14
B.1<AD<7
C.6<AD<8
D.12<AD<16
【答案】B
【解析】解:延长AD至点E,使AD=ED,连接BE、CE. ∵点D是BC的中点,
∴BD=CD,
∴四边形ABEC是平行四边形(对角线互相平分的四边形是平行四边形),
∴CE=AB(平行四边形的对边相等),
在△ACE中,CE﹣AC<AE<CE+AC,
即2<2AD<14,
1<AD<7.
故选B.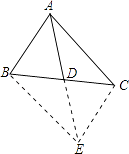
【考点精析】解答此题的关键在于理解三角形三边关系的相关知识,掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边,以及对平行四边形的判定与性质的理解,了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.

练习册系列答案
相关题目

