题目内容
 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.求证:OA平分∠BAC.
分析:先根据条件可以得出∠AEC=∠ADB=∠BEC=∠CDB=90°就可以得出△BCD≌△CBE,就有BD=CE,就可以得出OE=OD,再证明△ODA≌△OEA就可以得出∠DAO=∠EAO而得出结论.
解答:证明:∵CE⊥AB,BD⊥AC,
∴∠AEC=∠ADB=∠BEC=∠CDB=90°.
∵OB=OC,
∴∠DBC=∠ECB.
在△BCD和△CBE中,
,
∴△BCD≌△CBE(AAS),
∴BD=CE.
∵OB=OC,
∴BD-OB=EC-OC
∴OD=OE.
在Rt△ODA和Rt△OEA中,
,
∴Rt△ADO≌Rt△AEO(HL),
∴∠DAO=∠EAO,
∴OA平分∠BAC.
∴∠AEC=∠ADB=∠BEC=∠CDB=90°.
∵OB=OC,

∴∠DBC=∠ECB.
在△BCD和△CBE中,
|
∴△BCD≌△CBE(AAS),
∴BD=CE.
∵OB=OC,
∴BD-OB=EC-OC
∴OD=OE.
在Rt△ODA和Rt△OEA中,
|
∴Rt△ADO≌Rt△AEO(HL),
∴∠DAO=∠EAO,
∴OA平分∠BAC.
点评:本题考查了垂直的性质的运用,AAS,HL证明三角形全等的运用,等式的性质的运用,角平分线的判定的运用,解答时证明三角形是关键.

练习册系列答案
相关题目
 10、已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
10、已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC. 15、已知,如图,锐角△ABC中,AD⊥BC于D,H为垂心(三角形三条高线的交点);在AD上有一点P,且∠BPC为直角.
15、已知,如图,锐角△ABC中,AD⊥BC于D,H为垂心(三角形三条高线的交点);在AD上有一点P,且∠BPC为直角.
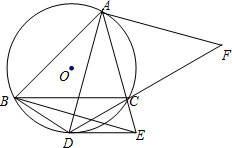 点D的切线DE交AC的延长线于点E,且DE∥BC;连接AD、BD、BE,AD的垂线AF与DC的延长线交于点F.
点D的切线DE交AC的延长线于点E,且DE∥BC;连接AD、BD、BE,AD的垂线AF与DC的延长线交于点F. 已知:如图,锐角△ABC内接于⊙O,∠ABC=45°;点D是
已知:如图,锐角△ABC内接于⊙O,∠ABC=45°;点D是